Lagrangian cloud model (LCM)

The LCM is based on the formulation of the LPM (Sect. lagrangian particle model). For the LCM, however, the Lagrangian particles are representing droplets and aerosols. The droplet advection and sedimentation is given by the Eqs. for du_p,i / dt and τ_p^-1 in Sect. formulation of the LPM with ρ_p,0 = ρ_l,0. At present it is computationally not feasible to simulate a realistic amount of particles. A single Lagrangian particle thus represents an ensemble of identical particles (i.e., same radius, velocity, mass of solute aerosol) and is referred to as "super-droplet". The number of particles in this ensemble is referred to as the "weighting factor". For example, q_l of a certain LES grid volume results from all Lagrangian particles located therein considering their individual weighting factor A_n:

with N_p being the number of particles inside the grid volume of size ΔV, and r_n being the radius of the particle. The concept of weighting factors and super-droplets in combination with LES has been also used similarly by Andrejczuk et al. (2208) and Shima et al. (2009) for warm clouds, as well as by Sölch and Kärcher (2010) for ice clouds.

Diffusional growth

The growth of a particle by diffusion of water vapor, i.e., condensation and evaporation, is described by

with the coefficients

depending primarily on the diffusion of water vapor in air and heat conductivity of air, respectively. f_v is the ventilation factor, which accounts for the increased diffusion of water vapor, particularly the accelerated evaporation of large drops precipitating from a cloud (e.g., Pruppacher and Klett, 1997, Chap. 13.2.3):

Here, Re_p is particle Reynolds number. The relative water supersaturation S is computed from the LES values of θ and q_v, tri-linearly interpolated to the particle's position. The equilibrium saturation term S_eq considers the impact of surface tension as well as the physical and chemical properties of the solute aerosol on the equilibrium saturation of the droplet. In order to take into account these effects, the optional activation model for fully soluble aerosols must be switched on:

with coefficients for surface tension

and physical and chemical properties

Here, ϑ is the temperature-dependent surface tension, and M_l = 18.01528 g mol^-1 the molecular mass of water. Depending on the simulation setup (e.g., continental or maritime conditions), the physical and chemical properties of the aerosol, its mass m_s, molecular mass M_s, and the van't Hoff factor F_vH, indicating the degree of the solute aerosol's dissociation, are prescribed. As discussed by Hoffmann et al. (2015), the aerosol mass (or equivalently aerosol radius) can be specified by an additional particle feature allowing the initialization of aerosol mass distributions, i.e., varying aerosol masses among the simulated particle ensemble.

In summary, diffusional growth is the major coupling between the LES and LCM model. The change of water vapor during one time step is considered in the prognostic equations for potential temperature (see Eq. three in Sect. governing equations) and water vapor mixing ratio (see Eq. four in Sect. governing equations) by

Here, r_n and r_n^∗ are the radius of the nth droplet before and after diffusional growth, respectively. Since the diffusional growth (see first Eq. in Sect. diffusional growth) is a stiff differential equation, we use a 4th-order Rosenbrock-method (Press et al., 1996; Grabowski et al., 2011), adapting its internal time step for both a computationally efficient and numerically accurate solution.

Collision and coalescence

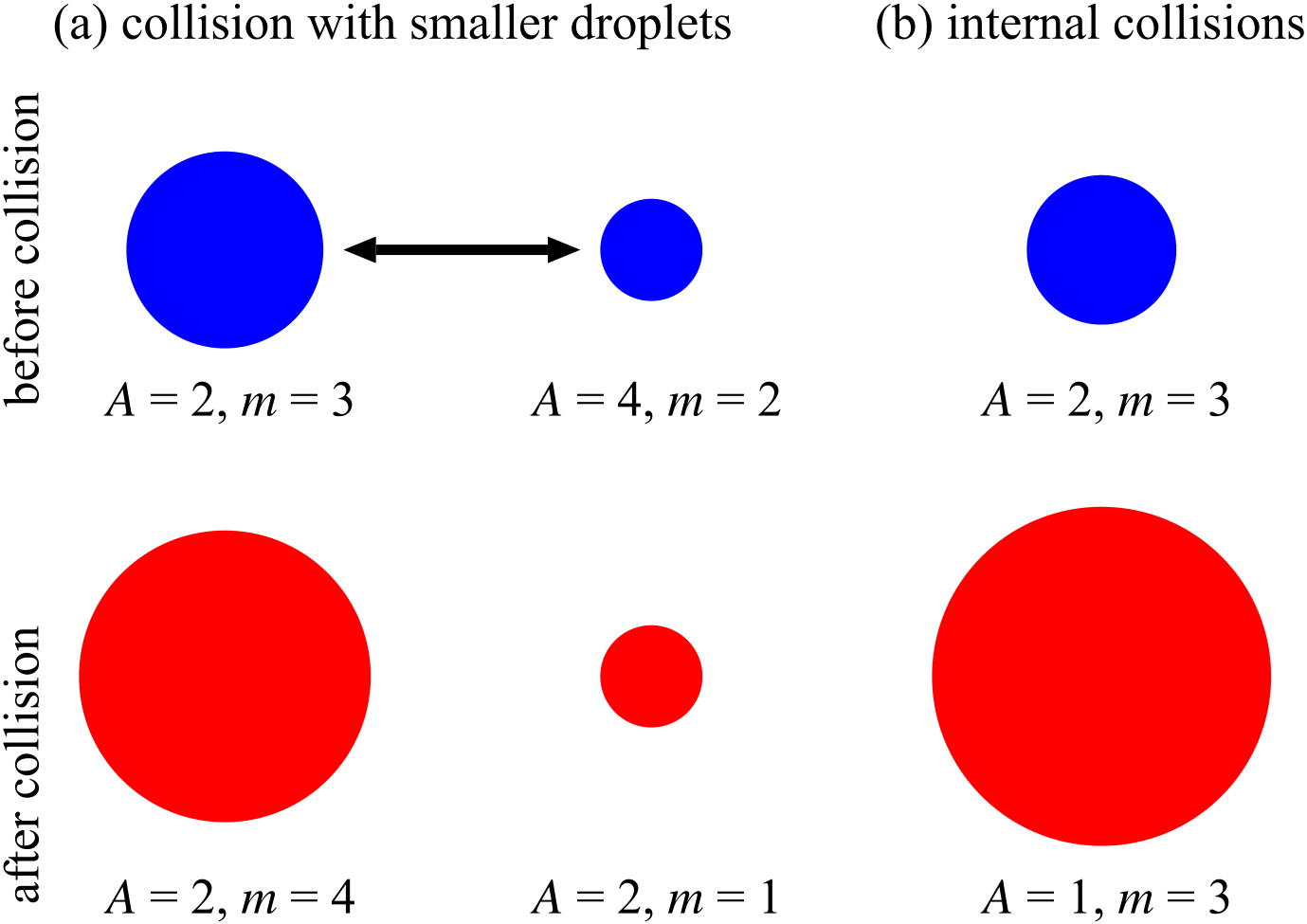
Collision and coalescence are computed using a statistical approach that allows the collision of all droplets that are currently located in the same LES grid volume. For this purpose, two quantities are predicted: the weighting factor, i.e., the number of droplets represented by a super-droplet, and the bulk mass of all droplets represented by a super droplet, m_n = A_n (4/3) π ρ_l r_n³. For the collision of a super-droplet with a super-droplet smaller in radius, we assume that the larger droplets merges with a certain amount of smaller droplets. Thereby, the weighting factor of the larger super-droplet is kept constant, while bulk mass and consequently radius increase (see Fig. 9a). On the other hand, the weighting factor and bulk mass of the smaller super-droplet decrease according to the amount of droplets lost to the larger super-droplet, keeping the smaller super-droplet's radius constant. As described in Riechelmann et al. (2015), we allow the droplets represented by a single super-droplet to collide among each other. These internal collisions only decrease the weighting factor of the super-droplet but not the bulk mass. Consequently, internal collisions increase the super-droplet's radius (see Fig. 9b). The collision kernel K, which describes the collision probability of two droplets, can either be a purely gravitational one (Hall, 1980) or including turbulence effects (Ayala et al., 2008).

We arrange the droplets by radius such that r_n ≤ r_n+1. The weighting factor after one collision/coalescence time step then reads as

The asterisk denotes a quantity after one collision/coalescence time step. On the right-hand side, we consider the initial weighting factor (first term), the loss of droplets due to internal collisions (second term), and the loss of droplets due to collision with all larger droplets (third term). Note that collision with smaller droplets does not change the weighting factor of the larger droplet.

Since the mass of all droplets represented by a~single super-droplet is not a~useful quantity, we predict the volume averaged radius of all droplets represented by a super-droplet directly:

On the right-hand side, the nominator (first pair of round brackets) contains the initial mass (first term), the gain of mass due to collisions with all smaller droplets (second term), and the loss of mass due to collisions with all larger droplets (third term). The denominator (second pair of round brackets) is identical to the Eq. for A_n^* above divided by A_n.

Figure 9: Illustration of (a) the collision of a super-droplet with a super-droplet smaller in radius, and (b) internal collisions of a single super-droplet. Blue (red) circles indicate super-droplets before (after) collision. Weighting factor (A), and bulk mass (m) are denoted in arbitrary units. The radius of the colored circle indicates the volume averaged radius of droplets represented by the super-droplet.

Recent applications

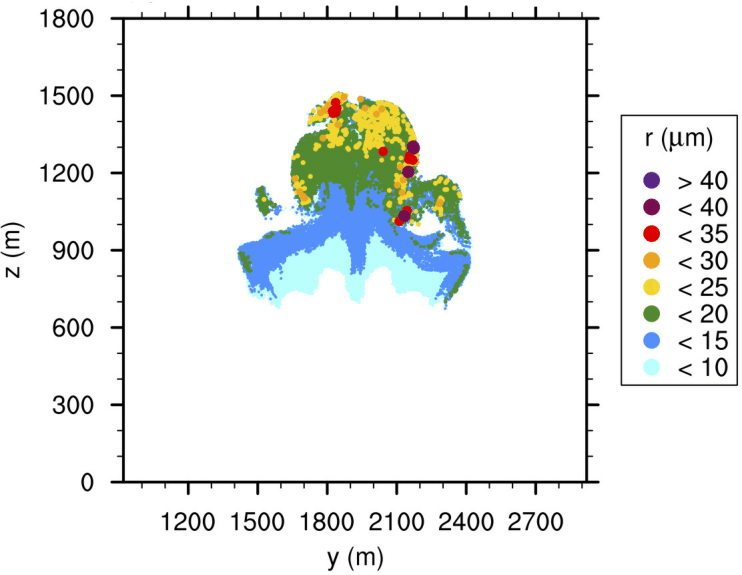
The LCM was validated against traditional bulk models for the BOMEX (The Barbados Oceanographic and Meteorological EXperiment) experiment (see Siebesma et al., 2003) by Riechelmann et al. (2012). Riechelmann et al. (2012) and Lee et al. (2014) used the LCM for studying turbulence and droplet dynamics in convective clouds; Hoffmann et al. (2015) investigated cloud droplet activation. Figure 10 shows the spatial distribution of simulated droplets and their respective radius within a simulated cumulus cloud. It appears that the largest drops (in terms of radius) are located at the top and the edges of the cloud, whereas smaller droplets tend to be located at the cloud base.

Figure 10: Distribution of droplets (colored dots) inside a shallow cumulus cloud simulated with PALM. The figure shows a vertical cross-section through the 3-D cloud. The color and size indicate the droplet's radius. The cloud has been triggered by a bubble of warm air (similar to Hoffmann et al., 2015). A grid spacing of 20 m was used and about 225 million particles were simulated in total.

References

• Andrejczuk M, Reisner JM, Henson B, Dubey MK, Jeffery CA. 2008. The potential impacts of pollution on a nondrizzling stratus deck: Does aerosol number matter more than type?. J. Geophys. Res. 113: D19204. ​doi.

• Shima S-I, Kusano K, Kawano A, Sugiyama T, Kawahara S. 2009. The super-droplet method for the numerical simulation of clouds and precipitation: a particle-based and probabilistic microphysics model coupled with a non-hydrostatic model. Q. J. Roy. Meteor. Soc. 135: 1307–1320.

• Sölch I, Kärcher B. 2010. A large-eddy model for cirrus clouds with explicit aerosol and ice microphysics and Lagrangian ice particle tracking. Q. J. Roy. Meteor. Soc. 136: 2074–2093.

• Pruppacher HR, and Klett JD. 1997. Microphysics of Clouds and Precipitation. 2nd Edn. Kluwer Academic Publishers. Dordrecht.

• Hoffmann F, Raasch S, Noh Y. 2015. Entrainment of aerosols and their activation in a shallow cumulus cloud studied with a coupled LCM-LES approach. Atmos. Res. 156: 43–57. ​doi

• Press WH, Teukolsky SA, Vetterling WT, and Flannery BP. 1996. Numerical Recipes in Fortran 90: the Art of Parallel Scientific Computing. 2nd Edn. Cambridge University Press. Cambridge.

• Grabowski WM, Andrejczuk M, Wang L-P. 2011. Droplet growth in a bin warm-rain scheme with Twomey CCN activation. Atmos. Res. 99: 290–301.

• Riechelmann T, Wacker U, Beheng KD, Etling D, Raasch S. 2015. Influence of turbulence on the drip growth in warm clouds, part II: Sensitivity studies with a spectral bin microphysics and a lagrangian cloud model. Meteorol. submitted.

• Hall WD. 1980. A detailed microphysical model within a two-dimensional dynamic framework: model description and preliminary results. J. Atmos. Sci. 37: 2486–2507.

• Ayala O, Rosa B, Wang L-P. 2008. Effects of turbulence on the geometric collision rate of sedimenting droplets. Part 2. Theory and parameterization. New J. Phys. 10: 075016. ​doi

• Siebesma AP, Bretherton CS, Brown A, Chlond A, Cuxart J, Duynkerke PG, Jiang H, Khairoutdinov M, Lewellen D, Moeng C-H, Sanchez E, Stevens B, Stevens, DE. 2003. A large eddy simulation intercomparison study of shallow cumulus convection. J.~Atmos.~Sci. 60: 1201–1219.

• Riechelmann T, Noh Y, Raasch S. 2012. A new method for large-eddy simulations of clouds with Lagrangian droplets including the effects of turbulent collision. New J. Phys. 14: 065008. ​doi

• Lee JH, Noh Y, Raasch S, Riechelmann T, Wang L-P. 2014. Investigation of droplet dynamics in a convective cloud using a Lagrangian cloud model. Meteorol. Atmos. Phys. 124: 1–21. ​doi