WP-S5.1: Uncertainty of model results depending on inaccurate input data
Goals of the project:
Uncertainty in the input data leads to uncertain model results. The aim of this project is to determine the necessary accuracy of the input data according to the size of their influence on the model results and to give recommendations for the necessary accuracy in data collection in order to optimally use the effort and costs associated with thorough data collection.
Tasks of the project:
The tasks of WP-S5.1 are structured into the following sub-work packages with the following tasks:
WP-S5.1.1: Studies for naturelike surfaces. In consultation with WP-S5.2 and users, it is worked out which uncertainties in the results are still tolerable for users. The magnitude of the inherent errors in data collection is used as the bandwidth in the simulations in order to determine the resulting errors for naturelike surfaces.
WP-S5.1.2: Studies for urban surfaces. In an urban environment, a large number of input variables have to be provided for the calculation of urban climate parameters. Again, a systematic study determines the range of the simulation results to be expected against the background of the individual uncertainties of the input parameters.
WP-S5.1.3: Studies for green and blue surfaces. Green elements in cities such as trees, facade greening, and water expanses are important elements for adapting the city to the consequences of climate change. Also for these parameters the input variables are only available with more or less great uncertainties. Sensitivity studies determine how exactly which parameters have to be available if a certain order of magnitude is expected in the result.
Project structure:
PI: Prof. Dr. Günter Groß.
Project scientist: Simone Pfau, M.Sc.
Deliverables:
Uncertainty and sensitivity analyses are to be carried out in order to determine the range of the model results depending on the uncertainty of the input data and the necessary accuracy of the input data to ensure the desired accuracy of the results.
Progress so far:
The progress made so far includes the selection of appropriate methods and the finished application of the Morris-Method. In addition, initial simulations to investigate the influence of input parameter uncertainties on those of the output parameters were conducted.
Several input parameters are varied simultaneously as part of the uncertainty analysis. Since this leads to a number of model runs that increase exponentially with the number of input parameters, it is useful to filter out those parameters that do not make a significant contribution to the uncertainty of the output. This is done using the Morris method. It requires a number of model runs that is linear in the number of inputs and is based on the idea that the difference between results with only one different input factor is a measure of how sensitive the result is to variation of that input factor. A number r of trajectories of sampling points is constructed in the parameter space, where two following points differ in only one input factor. This is used to calculate r measures for each input factor. The mean µ and the mean of the absolute measures µ* can be used to rank the input factors in order of importance for the uncertainty of the output. Additionally, the Bayesian approach will be used to estimate the allowed uncertainty in the input parameters to ensure the desired accuracy of the results. A prior probability distribution, which contains information on the input data, is updated with a so-called likelihood, the probability of obtaining a desired output with a wanted spread given some specific input. This leads to a posterior distribution that provides information about the variance of the input parameters given desired properties of the model outputs.
The Morris method was used for different setups, whereby model areas with horizontally homogeneous properties or individual obstacles were initially considered. The ‘land surface model’ and the ‘radiation model’ were used for horizontally homogeneous natural and urban surfaces, and the ‘vegetation_pars’ or ‘pavement_pars’ and the ‘soil_pars’ were varied. Using the ‘plant canopy model’, a horizontally homogeneous plant canopy was considered and the influence of its height, its LAD-profile and the canopy drag coefficient on the stationary wind profile were examined. Setups with single obstacles included a single building with varying dimensions or a single tree varying in height, crown height to width ratio, LAI, crown and trunk diameter, and canopy drag coefficient.
In addition to these simple setups, the influence of green and blue elements in an urban area is investigated in order to be able to adjust the accuracy and effort involved in data collection in urban areas accordingly. A grid sensitivity study has already been carried out for such a setup. The simulation of diurnal cycles and the uncertainty and sensitivity analysis are being carried out.
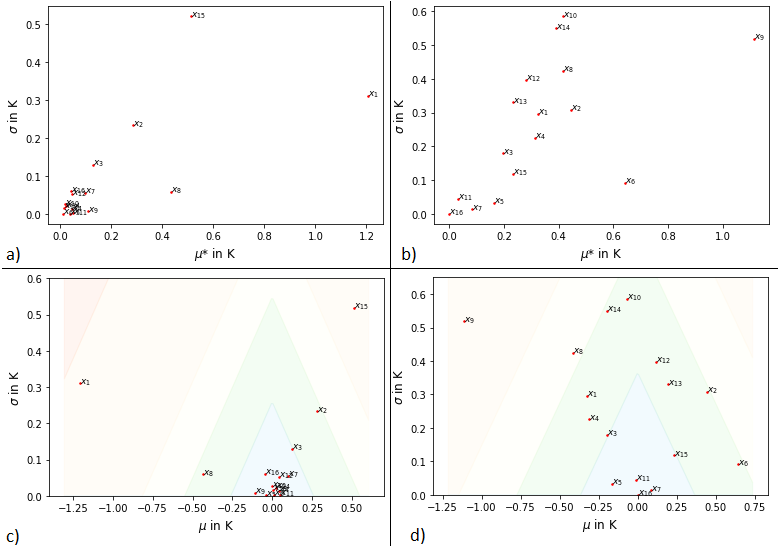
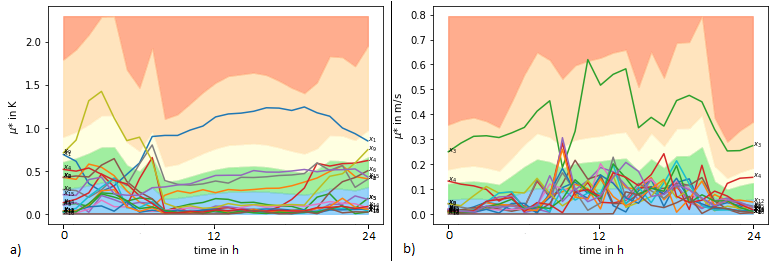
Fig. 1 and 2 show selected results for the application of the Morris method on the horizontally homogeneous natural surface. The assessment of the relevance of the parameters can be done using the standard deviation of the output σout. If a parameter leads to a variation of the output that corresponds to or exceeds , it can be assigned a relevance according to the prefactor z*σout, which is shown in color in Fig. 1 c), d) and Fig. 2.
Figure 1: Morris plots for the Morris measures with respect to the 2 m maximum (a, c) and minimum (b, d) of the potential temperature.
Figure 2: Diurnal cycles of the Morris measures µi* for different inputs xi for the horizontal mean of the 2 m potential temperature (a) and the 10 m windspeed (b).
References:
Allmaras et al.: Estimating parameters in physical models through Bayesian inversion a complete example, 2013.
Campolongo et al.: An effective screening design for sensitivity analysis of large models, 2006.
Groß: On the range of boundary layer model results depending on inaccurate input data, 2019.
Heldens, Wieke et al.: Geospatial input data for the PALM model system 6.0: model requirements, data sources and processing, https://doi.org/10.5194/gmd-13-5833-2020, 2020.
Hughes et al.: Global sensitivity analysis of England's housing energy model, 2015.
Laine et al.: Ensemble prediction and parameter estimation system: the method, 2012.
Lindauer: Dynamische Sensitivitätsanalysemethoden energetischer Wohngebäudequartierssimulationen, 2017.
Saltelli et al.: Sensitivity Analysis in Practice, 2004.
Soong-Oh Han: Varianzbasierte Sensitivitätsanalyse als Beitrag zur Bewertung der Zuverlässigkeit adaptronischer Struktursysteme, 2011.
Contacts:
gross[at]muk.uni-hannover.de
pfau[at]muk.uni-hannover.de
Attachments (2)
- WP_S51_figure2.png (94.7 KB) - added by hettrich 4 years ago.
- WP_S51_figure1.png (43.8 KB) - added by hettrich 4 years ago.
Download all attachments as: .zip