| Version 6 (modified by gronemeier, 7 years ago) (diff) |
|---|
Turbulence Parameterization ¶
Since r2696, PALM can be operated as a RANS (Reynolds-averaged Navier-Stokes) model. When running PALM as a RANS model, a different turbulence closure is used compared to the LES model where the turbulence kinetic energy (TKE) e is completely parameterized.
Two different turbulence models are available:
which are described below.
PALM is automatically switched into RANS mode if one of the above listed turbulence parameterizations is selected. The turbulence parameterization can be selected via the namelist parameter turbulence_closure.
Prior to r3545, the namelist parameter rans_mode needs to be set to .TRUE. in addition of selecting one of the turbulence parameterizations if the RANS mode shall be used.
TKE-l model ¶ ¶
The TKE-l model calculates the eddy diffusivities via the turbulence kinetic energy e and the mixing length l:
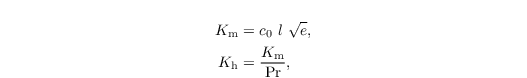
where Pr denotes the Prandtl number. The model constant c0 is set to 0.55 by default, but can be altered via the namelist parameter rans_const_c.
The TKE is calculated using the following prognostic equation:
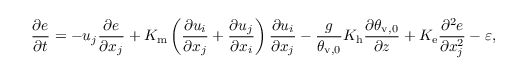
where Ke is defined as
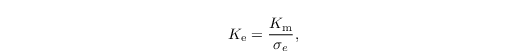
with σe = 1. This can be altered via the namelist parameter rans_const_sigma. The dissipation rate ε of the TKE is calculated via
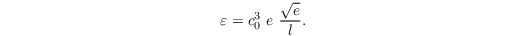
The mixing length is defined using the mixing length lB according to Blackadar (1962) and the Dyer-Businger function Φm

where κ, f, Ug, L, and z denote the von-Karman constant, the Coriolis parameter, the geostrophic wind, the Monin-Obukhov length, and the height, respectively. lwall defines an upper limit of the mixing length as the distance to the nearest solid surface (wall).
TKE-ε model ¶ ¶
The TKE-ε model calculates the eddy diffusivities via the turbulence kinetic energy e and the dissipation rate ε of the TKE:
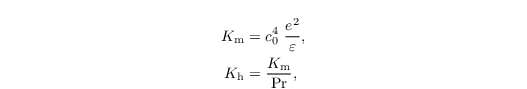
where Pr denotes the Prandtl number. The model constant c0 is set to 0.55 by default, but can be altered via the namelist parameter rans_const_c.
The TKE is calculated using the same prognostic equation as the TKE-l model. The dissipation rate ε is calculated via the following prognostic equation:
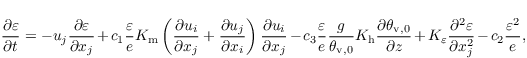
where Kε is defined as
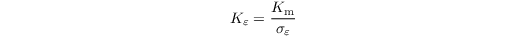
with σε = 1.3. This can be altered via the namelist parameter rans_const_sigma. The model constants c1, c2, and c3 are set to 1.44, 1.92, and 1.44, respectively. These values can be altered via the namelist parameter rans_const_c.
