doc/tec/turbulence_parameterization – PALM

Home

wiki:doc/tec/turbulence_parameterization

Context Navigation

Version 4 (modified by gronemeier, 6 years ago) (diff)
--

\varepsilon\varepsilon= Turbulence Paramereization =

Page is under construction!

Since r????, PALM can be operated as a RANS (Reynolds-averaged Navier-Stokes) model. When running PALM as a RANS model, a different turbulence closure is used compared to the LES model where the turbulence kinetic energy (TKE) e is completely parameterized.

Two different turbulence models are available:

which are described below.

TKE-l model

The TKE-l model uses the following prognostic equation to calculate e:

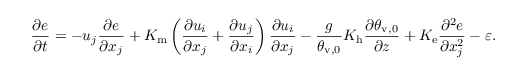
$\begin{equation*} \frac{\partial{e}}{\partial t} = - u_j\frac{\partial e}{\partial x_j} + K_\mathrm{m} \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right) \frac{\partial u_i}{\partial x_j} - \frac{g}{\theta_{\mathrm{v},0}} K_\mathrm{h} \frac{\partial \theta_{\mathrm{v},0}}{\partial z} + K_\mathrm{e} \frac{\partial^2 e}{\partial x_j^2} - \varepsilon. \end{equation*}$

where K_m, K_h, and K_e are the eddy diffusivities of momentum and heat, and the diffusivity coefficient of the TKE, respectively, which are calculated via

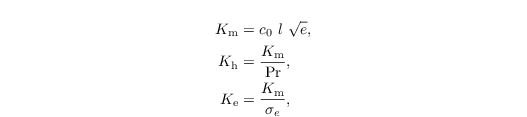
$\begin{align*} K_\mathrm{m} &= c_0 \ l \ \sqrt{e}, \\ K_\mathrm{h} &= \frac{K_\mathrm{m}}{\mathrm{Pr}}, \\ K_\mathrm{e} &= \frac{K_\mathrm{m}}{\sigma_e}, \end{align*}$

with σ_e = 1. This can be altered via the namelist parameter rans_const_sigma. Here, Pr and l denote the Prandtl number and mixing length, respectively. The model constant c₀ is set to 0.55 by default, but can be altered via the namelist parameter rans_const_c. The mixing length is defined using the mixing length l_B according to Blackadar (1962) and the Dyer-Businger function Φ_m

$\begin{align*} l &= \min\left( \frac{l_\mathrm{B}}{\Phi_\mathrm{m}}, l_\mathrm{wall} \right), \\ l_\mathrm{B} &= \dfrac{\kappa z}{1+\frac{\kappa z}{\lambda}}, \\ \lambda &= 2.7 \cdot 10^{-4} |U_g| f, \\ \Phi_\mathrm{m} &= 1+5\frac{z}{L}, \end{align*}$

where κ, f, U_g, L, and z denote the von-Karman constant, the Coriolis parameter, the geostrophic wind, the Monin-Obukhov length, and the height, respectively.

The dissipation rate of the TKE, ε, is calculated via

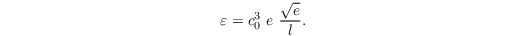
$\begin{equation*} \varepsilon = c_0^3 \ e \ \frac{\sqrt{e}}{l}. \end{equation*}$

TKE-ε model

The TKE-ε model uses an additional prognostic equation to calculate the dissipation rate ε of the TKE:

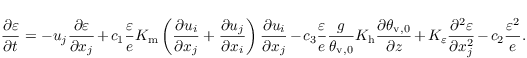
$\begin{equation*} \frac{\partial{\varepsilon}}{\partial t} = - u_j\frac{\partial \varepsilon}{\partial x_j} + c_1 \frac{\varepsilon}{e} K_\mathrm{m} \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right) \frac{\partial u_i}{\partial x_j} - c_3 \frac{\varepsilon}{e} \frac{g}{\theta_{\mathrm{v},0}} K_\mathrm{h} \frac{\partial \theta_{\mathrm{v},0}}{\partial z} + K_\varepsilon \frac{\partial^2 \varepsilon}{\partial x_j^2} - c_2 \frac{\varepsilon^2}{e}. \end{equation*}$

The diffusivity coefficient K_ε is defined as

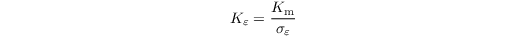
$\begin{equation*} K_\varepsilon = \frac{K_\mathrm{m}}{\sigma_\varepsilon} \end{equation*}$

with σ_ε = 1.3. This can be altered via the namelist parameter rans_const_sigma.

Download in other formats:

Plain Text