Home

Context Navigation

Version 5 (modified by Giersch, 9 years ago) (diff)
--

This site is currently under construction!

Turbulence closure

One of the main challenges in LES modeling is the turbulence closure. The filtering process yields four SGS covariance terms (see the first five equations at governing equations) that cannot be explicitly calculated. In PALM, these SGS terms are parametrized using a 1.5-order closure after Deardorff (1980). PALM uses the modified version of Moeng and Wyngaard (1988) and Saiki et al. (2000). The closure is based on the assumption that the energy transport by SGS eddies is proportional to the local gradients of the mean quantities and reads

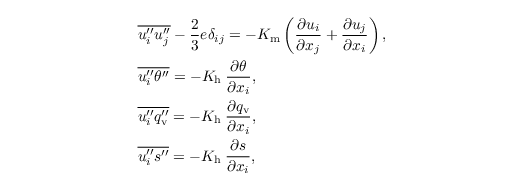
$\begin{align*} & \overline{u_i^{\prime\prime} u_j^{\prime\prime}} - \frac{2}{3} e \delta_{ij} = -K_\mathrm{m} \left(\frac{\partial u_{i}} {\partial x_{j}} + \frac{\partial u_j} {\partial x_{i}}\right),\,\\ & \overline{u^{\prime\prime}_{i}\theta^{\prime\prime}} = -K_\mathrm{h} \:\frac{\partial \theta} {\partial x_{i}},\,\\ & \overline{u^{\prime\prime}_{i}q^{\prime\prime}_\mathrm{v}} = -K_\mathrm{h} \:\frac{\partial q_\mathrm{v}} {\partial x_{i}},\,\\ & \overline{u^{\prime\prime}_{i}s^{\prime\prime}} = -K_\mathrm{h} \:\frac{\partial s}{\partial x_{i}},\, \end{align*}$

where K_m and K_h are the local SGS eddy diffusivities of momentum and heat, respectively. They are related to the SGS-TKE as follows

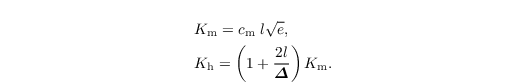
$\begin{align*} &K_\mathrm{m} = c_\mathrm{m}\;l\sqrt{e},\\ & K_\mathrm{h} = \left(1+\frac{2l}{\boldsymbol{\varDelta}}\right) K_\mathrm{m}. \end{align*}$

Here, c_m = 0.1 is a model constant and Δ = (Δx Δy Δz)^1/3 with Δx, Δy, Δz being the grid spacings in x, y and z direction, respectively. The SGS mixing length l depends on height z (distance from the wall when topography is used), Δ, and stratification and is calculated as

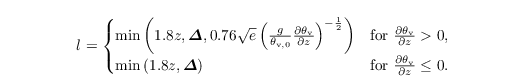
$\begin{align*} & l = \begin{cases} \min\left(1.8z,\boldsymbol{\varDelta}, 0.76\sqrt{e}\left(\frac{g}{\theta_{\mathrm{v},0}} \frac{\partial{\theta_{\mathrm{v}}}}{\partial z}\right)^{-\frac{1}{2}} \right) &\text{for~} \frac{\partial{\theta_{\mathrm{v}}}}{\partial z} > 0, \\ \min\left(1.8z, \boldsymbol{\varDelta}\right) &\text{for~} \frac{\partial{\theta_{\mathrm{v}}}}{\partial z} \leq 0. \end{cases} \end{align*}$

Moreover, the closure includes a prognostic equation for the SGS-TKE:

$\begin{align*} & \frac{\partial{e}}{\partial t} = - u_j\frac{\partial e}{\partial x_j} - \left(\overline{u_i^{\prime\prime} u_j^{\prime\prime}}\right)\frac{\partial u_i} {\partial x_j} + \frac{g}{\theta_{\mathrm{v},0}}\overline{u_3^{\prime\prime} {\theta_{\mathrm{v}}}^{\prime\prime}}-\frac{\partial}{\partial x_j} \left[\overline{u_j^{\prime\prime} \left(e + \frac{p^{\prime\prime}}{\rho_0}\right)}\right] - \epsilon. \end{align*}$

The pressure term in the equation above is parametrized as

$\begin{align*} &\left[\overline{u_j^{\prime\prime} \left(e + \frac{p^{\prime\prime}}{\rho_0}\right)}\right] = -2 K_\mathrm{m} \frac{\partial e}{\partial x_j} \end{align*}$

and ε is the SGS dissipation rate within a grid volume, given by

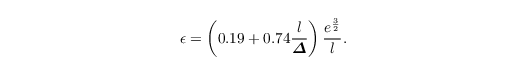
$\begin{align*} & \epsilon=\left(0.19 + 0.74\frac{l}{\boldsymbol{\varDelta}}\right)\frac{e^{\frac{3}{2}}}{l}. \end{align*}$

Since θ_v depends on θ, q_v, and q_l (see last equation at governing equations), the vertical SGS buoyancy flux depends on the respective SGS fluxes (Stull, 1988, Chap. 4.4.5):

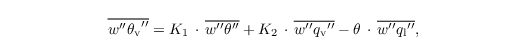
$\begin{align*} & \overline{w^{\prime\prime} {\theta_{\mathrm{v}}}^{\prime\prime}}=K_1\,\cdot\,\overline{w^{\prime\prime} {\theta}^{\prime\prime}} + K_2\,\cdot\,\overline{w^{\prime\prime} {q_\mathrm{v}}^{\prime\prime}}- \theta\,\cdot\,\overline{w^{\prime\prime} {q_\mathrm{l}}^{\prime\prime}}, \end{align*}$

with

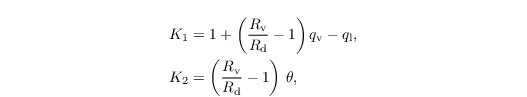
$\begin{align*} & K_1 =1+\left(\frac{R_\mathrm{v}}{R_\mathrm{d}}-1\right) q_\mathrm{v} - q_\mathrm{l},\\ & K_2 =\left(\frac{R_\mathrm{v}}{R_\mathrm{d}}-1\right)\,\theta, \end{align*}$

and the vertical SGS flux of liquid water, calculated as

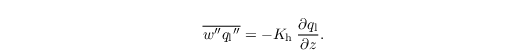
$\begin{align*} & \overline{w^{\prime\prime} {q_\mathrm{l}}^{\prime\prime}} = -K_\mathrm{h} \:\frac{\partial q_\mathrm{l}} {\partial z}. \end{align*}$

Note that this parametrization of the SGS buoyancy flux differs from that used with bulk cloud microphysics (see Sect. cloud microphysics).

References

Deardorff JW. 1980. Stratocumulus-capped mixed layers derived from a three-dimensional model. Bound.-Lay. Meteorol. 18: 495–527.

Moeng CH, Wyngaard JC. 1988. Spectral analysis of large-eddy simulations of the convective boundary layer. J. Atmos. Sci. 45: 3573–3587.

Saiki EM, Moeng CH, Sullivan PP. 2000. Large-eddy simulation of the stably stratified planetary boundary layer. Bound.-Lay. Meteorol. 95: 1–30.

Stull RB. 1988. An Introduction to Boundary Layer Meteorology, Kluwer Academic Publishers. Dordrecht. 666 pp.

Download in other formats:

Plain Text