| Version 8 (modified by Giersch, 9 years ago) (diff) |
|---|
This site is currently under construction!
Cloud mircrophysics
PALM offers an embedded bulk cloud microphysics representation that takes into account the liquid water specific humidity and warm (i.e., no ice) cloud-microphysical processes. Therefore, PALM solves the prognostic equations for the total water content
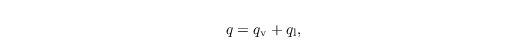
instead of qv, and for a linear approximation of the liquid water potential temperature (e.g., Emanuel, 1994)
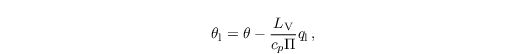
instead of θ as described in Sect. governing equations. Since q and θl are conserved quantities for wet adiabatic processes, condensation/evaporation is not considered for these variables.
Liquid phase microphysics are parametrized following the two-moment scheme of Seifert and Beheng (2001,2006), which is based on the separation of the droplet spectrum into droplets with radii < 40 μm (cloud droplets) and droplets with radii ≥ 40 μm (rain droplets). The model predicts the first two moments of these partial droplet spectra, namely cloud and rain droplet number concentration (Nc and Nr, respectively) as well as cloud and rain water specific humidity (qc and qr, respectively). Consequently, ql is the sum of both qc and qr. The moments' corresponding microphysical tendencies are derived by assuming the partial droplet spectra to follow a gamma distribution that can be described by the predicted quantities and empirical relationships for the distribution's slope and shape parameters. For a detailed derivation of these terms, see Seifert and Beheng (2001,2006).
We employ the computational efficient implementation of this scheme as used in the UCLA-LES (Savic-Jovcic and Stevens, 2008) and DALES (Heus et al., 2010) models. We thus solve only two additional prognostic equations for Nr and qr:
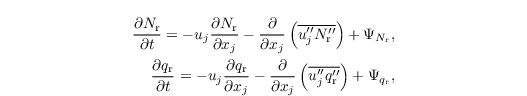
with the sink/source terms ΨNr and Ψqr, and the SGS fluxes
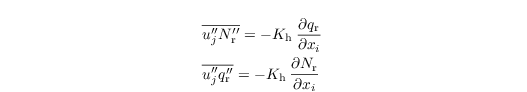
with Nc and qc being a fixed parameter and a diagnostic quantity, respectively.
In the next subsections we will describe the diagnostic determination of qc. From Sect. autoconversion on, the microphysical processes considered in the sink/source terms of θl, q, Nr and qr,
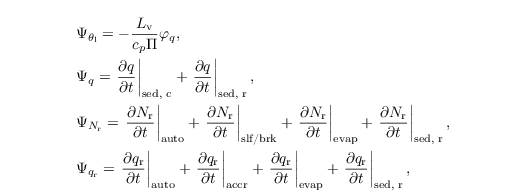
are used in the formulations of Seifert and Beheng (2006) unless explicitly specified. Section turbulence closure gives an overview of the necessary changes for the turbulence closure (cf. Sect. turbulence closure) using q and θl instead of qv and $θ$, respectively.
Diffusional growth of cloud water
The diagnostic estimation of qc is based on the assumption that water supersaturations are immediately removed by the diffusional growth of cloud droplets only. This can be justified since the bulk surface area of cloud droplets exceeds that of rain drops considerably (Stevens and Seifert, 2008). Following this saturation adjustment approach, qc is obtained by
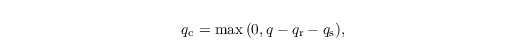
where qs is the saturation specific humidity. Because qs is a function of T (not predicted), qs is computed from the liquid water temperature Tl = Π θl in a first step:
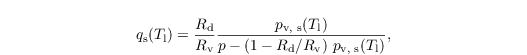
using an empirical relationship for the saturation water vapor pressure pv,s (Bougeault, 1981):
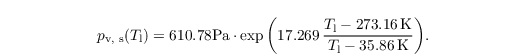
qs(T) is subsequently calculated from a 1st-order Taylor series expansion of qs at Tl (Sommeria and Deardorff, 1977):
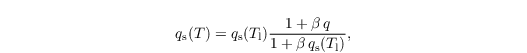
with
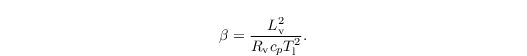
Autoconversion
In the following Sects. Autoconversion - Self-collection and breakup we describe collision and coalescence processes by applying the stochastic collection equation (e.g., Pruppacher and Klett, 1997, Chap. 15.3) in the framework of the described two-moment scheme. As two species (cloud and rain droplets, hereafter also denoted as c and r, respectively) are considered only, there are three possible interactions affecting the rain quantities: autoconversion, accretion, and selfcollection. Autoconversion summarizes all merging of cloud droplets resulting in rain drops (c + c → r). Accretion describes the growth of rain drops by the collection of cloud droplets (r + c → r). Selfcollection denotes the merging of rain drops (r + r → r).
The local temporal change of qr due to autoconversion is
![\begin{align*}
& \left.\frac{\partial q_\mathrm{r}}{\partial t}
\right|_{\text{auto}}=\frac{K_{\text{auto}}}{20\,m_{\text{sep}}}\frac{(\mu_\mathrm{c} +2)
(\mu_\mathrm{c} +4)}{(\mu_\mathrm{c} + 1)^2} q_\mathrm{c}^2
m_\mathrm{c}^2 \cdot \left[1+
\frac{\Phi_{\text{auto}}(\tau_\mathrm{c})}{(1-\tau_\mathrm{c})^2}\right]
\rho_0.
\end{align*}](/trac/tracmath/ef58d69eeb8e613e0b970b3700a2e0ec2f7754c5.png)
Assuming that all new rain drops have a radius of 40 μm corresponding to the separation mass msep = 2.6 x 10-10 kg, the local temporal change of Nr is
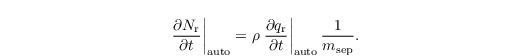
Here, Kauto = 9.44 x 109 m3 kg-2 s-1 is the autoconversion kernel, μc = 1 is the shape parameter of the cloud droplet gamma distribution and mc = ρ qc / Nc is the mean mass of cloud droplets. τc = 1 - qc / (qc + qr) is a dimensionless timescale steering the autoconversion similarity function
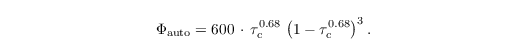
The increase of the autoconversion rate due to turbulence can be considered optionally by an increased autoconversion kernel depending on the local kinetic energy dissipation rate after Seifert et al. (2010).
Accretion
The increase of qr by accretion is given by:
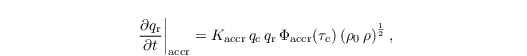
with the accretion kernel Kaccr = 4.33 m3 kg-1 s-1 and the similarity function
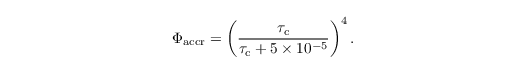
Turbulence effects on the accretion rate can be considered after using the kernel after Seifert et al. (2010).
Self-collection and breakup
Selfcollection and breakup describe merging and splitting of rain drops, respectively, which affect the rain water drop number concentration only. Their combined impact is parametrized as
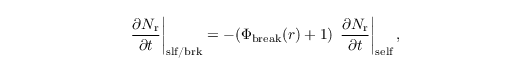
with the breakup function
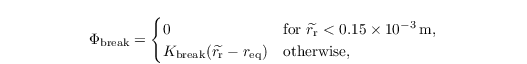
depending on the volume averaged rain drop radius
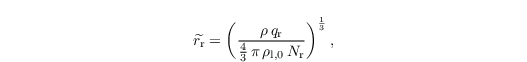
the equilibrium radius req = 550 x 10-6 m and the breakup kernel Kbreak = 2000 m-1. The local temporal change of Nr due to selfcollection is
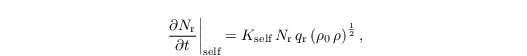
with the selfcollection kernel Kself = 7.12 m3 kg-1 s-1.
Evaporation of rainwater
Sedimentation of rainwater
Turbulence closure
Recent applications
References
- Emanuel KA. 1994. Atmospheric Convection. Oxford University Press.
- Seifert A, Beheng KD. 2001. A double-moment parameterization for simulating autoconversion, accretion and selfcollection. Atmos. Res. 59: 265–281.
- Seifert A, Beheng KD. 2006. A two-moment cloud microphysics parameterization for mixed-phase clouds. Part 1: Model description. Meteorol. Atmos. Phys. 92: 45–66.
- Savic-Jovcic V, Stevens B. 2008. The structure and mesoscale organization of precipitating stratocumulus. J. Atmos. Sci. 65: 1587–1605. doi
- Heus T, van Heerwaarden CC, Jonker HJJ, Pier Siebesma A, Axelsen S, van den Dries K, Geoffroy O, Moene AF, Pino D, de Roode SR, Vilà-Guerau de Arellano J. 2010. Formulation of the Dutch Atmospheric Large-Eddy Simulation (DALES) and overview of its applications. Geosci. Model Dev. 3: 415–444. doi
- Stevens B, Seifert A. 2008. Understanding macrophysical outcomes of microphysical choices in simulations of shallow cumulus convection. J. Meteor. Soc. Jpn. 86: 143–162.
- Bougeault, P. 1981. Modeling the trade-wind cumulus boundary layer. Part I: Testing the ensemble cloud relations against numerical data. J. Atmos. Sci. 38: 2414–2428.
- Sommeria G, Deardorff JW. 1977. Subgrid-scale condensation in models of nonprecipitating clouds. J. Atmos. Sci. 34: 344–355.
- Pruppacher HR, and Klett JD. 1997. Microphysics of Clouds and Precipitation. 2nd Edn. Kluwer Academic Publishers. Dordrecht.
- Seifert A, Nuijens L, Stevens B. 2010. Turbulence effects on warm-rain autoconversion in precipitating shallow convection. Q. J. Roy. Meteor. Soc. 136: 1753–1762.
Attachments (8)
-
Table4.png
(114.2 KB) -
added by Giersch 9 years ago.
List of cloud physics parameters and symbols
-
Table5.png
(38.6 KB) -
added by Giersch 9 years ago.
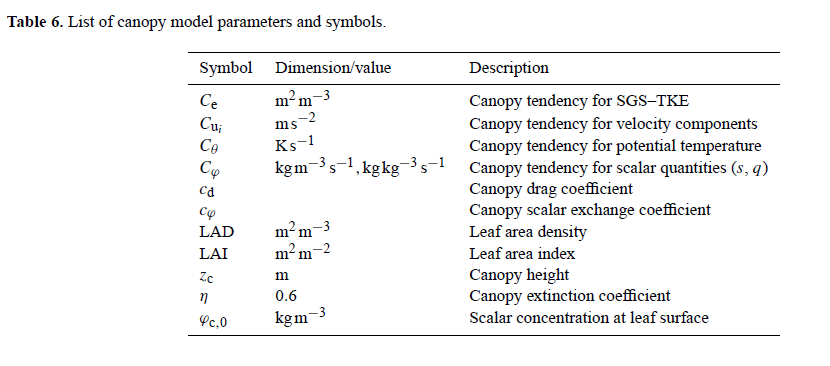
List of LPM symbols and parameters
-
Table6.png
(32.0 KB) -
added by Giersch 9 years ago.
List of canopy model parameters and symbols
-
06.png
(3.0 MB) -
added by Giersch 9 years ago.
Snapshot of the cloud field from a PALM run for.
- Button_Example.png (56.3 KB) - added by westbrink 6 years ago.
- Button_InputPara.png (57.8 KB) - added by westbrink 6 years ago.
- Button_Overview.png (56.0 KB) - added by westbrink 6 years ago.
- Button_References.png (55.5 KB) - added by westbrink 6 years ago.