Home

Context Navigation

Version 39 (modified by schwenkel, 7 years ago) (diff)
--

Cloud mircrophysics

PALM offers an embedded bulk cloud microphysics representation that takes into account warm (i.e., no ice) cloud-microphysical processes. Therefore, PALM solves the prognostic equations for the total water mixing ratio

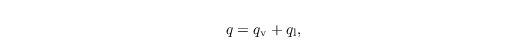
$\begin{align*} & q = q_\mathrm{v} + q_\mathrm{l}, \end{align*}$

instead of q_v, and for a linear approximation of the liquid water potential temperature (e.g., Emanuel, 1994)

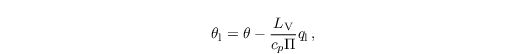
$\begin{align*} \theta_\mathrm{l} = \theta - \frac{L_\mathrm{V}}{c_p \Pi} q_\mathrm{l}\,, \end{align*}$

instead of θ as described in Sect. governing equations. Since q and θ_l are conserved quantities for wet adiabatic processes, condensation/evaporation is not considered for these variables.

PALM offers three different schemes (Kessler (1969), Seifert and Beheng (2001,2006), Morrison (2007)) for the treatment of liquid phase microphysics. The Kessler (1969) scheme provides a computational inexpensive way for the bulk microphysics. However, it only converts supersaturation into liquid water and considering autoconversion after a parameterization of Kessler (1969).

A more detailed parameterization is given by following the two-moment scheme of Seifert and Beheng (2001,2006), which is based on the separation of the droplet spectrum into droplets with radii < 40 μm (cloud droplets) and droplets with radii ≥ 40 μm (rain droplets). Here, the model predicts the first two moments of these partial droplet spectra, namely cloud and rain droplet number concentration (N_c and N_r, respectively) as well as cloud and rain water mixing ratio (q_c and q_r, respectively). Consequently, q_l is the sum of both q_c and q_r. The moments' corresponding microphysical tendencies are derived by assuming the partial droplet spectra to follow a gamma distribution that can be described by the predicted quantities and empirical relationships for the distribution's slope and shape parameters. For a detailed derivation of these terms, see Seifert and Beheng (2001,2006).

We employ the computational efficient implementation of this scheme as used in the UCLA-LES (Savic-Jovcic and Stevens, 2008) and DALES (Heus et al., 2010) models. We thus solve only two additional prognostic equations for N_r and q_r:

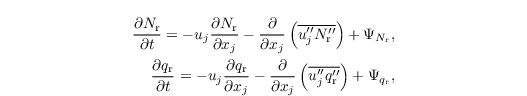
$\begin{align*} \frac{\partial N_\mathrm{r}}{\partial t} = - u_j \frac{\partial N_\mathrm{r}}{\partial x_j} - \frac{\partial}{\partial x_j}\left(\overline{u_j^{\prime\prime}N_\mathrm{r}^{\prime\prime}}\right) + \Psi_{N_\mathrm{r}},\\ \frac{\partial q_\mathrm{r}}{\partial t} = - u_j \frac{\partial q_\mathrm{r}}{\partial x_j} - \frac{\partial}{\partial x_j}\left(\overline{u_j^{\prime\prime}q_\mathrm{r}^{\prime\prime}}\right) + \Psi_{q_\mathrm{r}}, \end{align*}$

with the sink/source terms Ψ_Nr and Ψ_qr, and the SGS fluxes

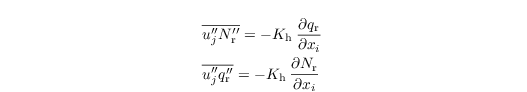
$\begin{align*} & \overline{u_j^{\prime\prime}N_\mathrm{r}^{\prime\prime}} = -K_\mathrm{h} \:\frac{\partial q_\mathrm{r}} {\partial x_{i}}\,\\ & \overline{u_j^{\prime\prime}q_\mathrm{r}^{\prime\prime}} = -K_\mathrm{h} \:\frac{\partial N_\mathrm{r}} {\partial x_{i}}\, \end{align*}$

with N_c and q_c being a fixed parameter and a diagnostic quantity, respectively.

The Morrison (2007) microphysics scheme can be understood as an extension of the scheme of Seifert and Beheng (2001,2006), where N_c and q_c are prognostic quantities as well. Moreover, using the Morrison (2007) scheme includes an explicit calculation of diffusional growth and an activation parameterization.

In the next subsections we will describe the diagnostic/prognostic determination (in dependence of the chosen scheme) of q_c. From Sect. autoconversion on, the microphysical processes considered in the sink/source terms of θ_l, q, N_r and q_r, as well as N_c and q_c for the Morrison (2007) scheme.

$\begin{align*} & \Psi_{\theta_\mathrm{l}} = - \frac{L_\mathrm{v}}{c_p \Pi} \varphi_q,\\ & \Psi_{q} = \left.\frac{\partial q}{\partial t} \right|_\text{sed, c} + \left.\frac{\partial q}{\partial t} \right|_\text{sed, r},\\ & \Psi_{N_\mathrm{r}} = \left.\frac{\partial N_\mathrm{r}}{\partial t} \right|_{\text{auto}}+ \left.\frac{\partial N_\mathrm{r}}{\partial t} \right|_\text{slf/brk}+ \left.\frac{\partial N_\mathrm{r}}{\partial t} \right|_{\text{evap}}+ \left.\frac{\partial N_\mathrm{r}}{\partial t} \right|_\text{sed, r},\\ & \Psi_{q_\mathrm{r}} = \left.\frac{\partial q_\mathrm{r}}{\partial t} \right|_{\text{auto}} + \left.\frac{\partial q_\mathrm{r}}{\partial t} \right|_{\text{accr}}+ \left.\frac{\partial q_\mathrm{r}}{\partial t} \right|_{\text{evap}}+ \left.\frac{\partial q_\mathrm{r}}{\partial t} \right|_\text{sed, r},\\ & \Psi_{N_\mathrm{c}} = \left.\frac{\partial N_\mathrm{c}}{\partial t} \right|_{\text{acti}}+ \left.\frac{\partial N_\mathrm{c}}{\partial t} \right|_\text{auto}+ \left.\frac{\partial N_\mathrm{c}}{\partial t} \right|_{\text{evap}}+ \left.\frac{\partial N_\mathrm{c}}{\partial t} \right|_\text{sed, c},\\ & \Psi_{q_\mathrm{c}} = \left.\frac{\partial q_\mathrm{c}}{\partial t} \right|_{\text{auto}} + \left.\frac{\partial q_\mathrm{c}}{\partial t} \right|_{\text{accr}}+ \left.\frac{\partial q_\mathrm{c}}{\partial t} \right|_{\text{cond,evap}}+ \left.\frac{\partial q_\mathrm{c}}{\partial t} \right|_\text{sed, c}, \end{align*}$

are used in the formulations of Seifert and Beheng (2006) unless explicitly specified. Section turbulence closure gives an overview of the necessary changes for the turbulence closure (cf. Sect. turbulence closure) using q and θ_l instead of q_v and θ, respectively.

Activation of cloud droplets

The use of the Morrison et al (2007) enables a prognostic equation for the cloud droplet number concentration. Here, it is assumed that cloud droplets are activated in dependence of the current supersaturation. This basic method is called Twomey activation scheme with the general form of

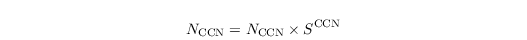
$\begin{align*} & N_\mathrm{CCN}=N_\mathrm{CCN} \times S^\mathrm{CCN} \end{align*}$

In PALM the supersaturation is calculated explicitly by tge thermodynamic fields of potential temperature and water vapor mixing ratio.

Diffusional growth of cloud water

By the usage of Seifert and Beheng (2001,2006) scheme the diagnostic estimation of q_c is based on the assumption that water supersaturations are immediately removed by the diffusional growth of cloud droplets only. This can be justified since the bulk surface area of cloud droplets exceeds that of rain drops considerably (Stevens and Seifert, 2008). Following this saturation adjustment approach, q_c is obtained by

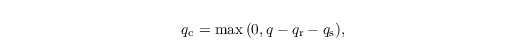
$\begin{align*} & q_\mathrm{c}=\max{\left(0, q - q_\mathrm{r} - q_\mathrm{s} \right)}, \end{align*}$

where q_s is the saturation mixing ratio. Because q_s is a function of T (not predicted), q_s is computed from the liquid water temperature T_l = Π θ_l in a first step:

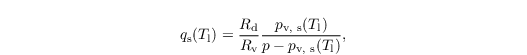
$\begin{align*} q_\mathrm{s}(T_\mathrm{l}) = \frac{R_\mathrm{d}}{R_\mathrm{v}} \frac{p_\text{v, s}(T_\mathrm{l})}{p - p_\text{v, s}(T_\mathrm{l})}, \end{align*}$

using an empirical relationship for the saturation water vapor pressure p_v,s (Bougeault, 1981):

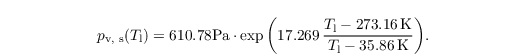
$\begin{align*} & p_\text{v, s}(T_\mathrm{l}) = 610.78 \text{Pa} \cdot \exp{\left(17.269\,\frac{T_\mathrm{l}-273.16\,\text{K}}{T_\mathrm{l}-35.86\,\text{K}} \right)}. \end{align*}$

q_s(T) is subsequently calculated from a 1st-order Taylor series expansion of q_s at T_l (Sommeria and Deardorff, 1977):

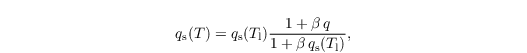
$\begin{align*} & q_\mathrm{s}(T)=q_\mathrm{s}(T_\mathrm{l})\frac{1+\beta\,q}{1+ \beta\,q_\mathrm{s}(T_\mathrm{l})}, \end{align*}$

with

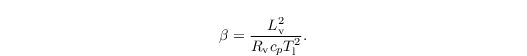
$\begin{align*} & \beta = \frac{L_\mathrm{v}^2}{R_\mathrm{v} c_p T_\mathrm{l}^2}. \end{align*}$

In contrast to that an explicit approach for the diffusional growth is applied in case of Morrison et al (2007). The condensation rate is calculated follwoing Khairoutdinov and Kogan (2000) and given by

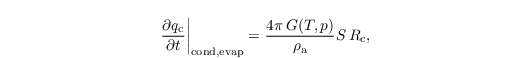
$\begin{align*} & \left.\frac{\partial q_\mathrm{c}}{\partial t} \right|_{\text{cond,evap}}= \frac{4 \pi\,G(T,p)}{\rho_\mathrm{a}}S\, R_\mathrm{c}, \end{align*}$

where S is the supersaturation, R_c the integral radius and G(T,p) a function of temperature and pressure considering heat conductivity and diffusion. Using this explicit approach the used timestep must fulfill a new criterion, since it is assumed that the supersaturation is constant during one timestep. The typical diffusion timescale is given by Arnason and Brown (1971) with

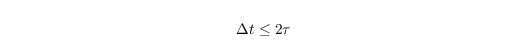
$\begin{align*} & \Delta t \leq 2 \tau \end{align*}$

with

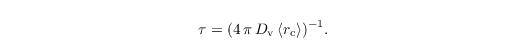
$\begin{align*} & \tau = (4\, \pi\,D_\mathrm{v}\,\langle r_\mathrm{c}\rangle)^{-1}. \end{align*}$

However, in PALM this criterion is not explicitly checked. Too ensure that unrealistic condensation or evaporation rates are avoided this scheme is limited to the value of the saturation-adjustment scheme.

Autoconversion

In the following Sects. Autoconversion - Self-collection and breakup we describe collision and coalescence processes by applying the stochastic collection equation (e.g., Pruppacher and Klett, 1997, Chap. 15.3) in the framework of the described two-moment scheme. As two species (cloud and rain droplets, hereafter also denoted as c and r, respectively) are considered only, there are three possible interactions affecting the rain quantities: autoconversion, accretion, and selfcollection. Autoconversion summarizes all merging of cloud droplets resulting in rain drops (c + c → r). Accretion describes the growth of rain drops by the collection of cloud droplets (r + c → r). Selfcollection denotes the merging of rain drops (r + r → r).

The local temporal change of q_r due to autoconversion is

$\begin{align*} & \left.\frac{\partial q_\mathrm{r}}{\partial t} \right|_{\text{auto}}=\frac{K_{\text{auto}}}{20\,m_{\text{sep}}}\frac{(\mu_\mathrm{c} +2) (\mu_\mathrm{c} +4)}{(\mu_\mathrm{c} + 1)^2} q_\mathrm{c}^2 m_\mathrm{c}^2 \cdot \left[1+ \frac{\Phi_{\text{auto}}(\tau_\mathrm{c})}{(1-\tau_\mathrm{c})^2}\right] \rho_0. \end{align*}$

Assuming that all new rain drops have a radius of 40 μm corresponding to the separation mass m_sep = 2.6 x 10^-10 kg, the local temporal change of N_r is

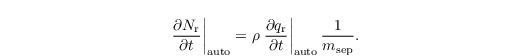
$\begin{align*} & \left.\frac{\partial N_\mathrm{r}}{\partial t} \right|_{\text{auto}}= \rho \left.\frac{\partial q_\mathrm{r}}{\partial t} \right|_{\text{auto}} \frac{1}{m_{\text{sep}}}. \end{align*}$

Here, K_auto = 9.44 x 10⁹ m³ kg^-2 s^-1 is the autoconversion kernel, μ_c = 1 is the shape parameter of the cloud droplet gamma distribution and m_c = ρ q_c / N_c is the mean mass of cloud droplets. τ_c = 1 - q_c / (q_c + q_r) is a dimensionless timescale steering the autoconversion similarity function

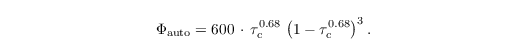
$\begin{align*} & \Phi_{\text{auto}}=600\,\cdot\,\tau_\mathrm{c}^{0.68}\,\left(1-\tau_\mathrm{c}^{0.68}\right)^3. \end{align*}$

The increase of the autoconversion rate due to turbulence can be considered optionally by an increased autoconversion kernel depending on the local kinetic energy dissipation rate after Seifert et al. (2010).

Accretion

The increase of q_r by accretion is given by:

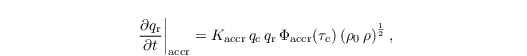
$\begin{align*} & \left.\frac{\partial q_\mathrm{r}}{\partial t} \right|_{\text{accr}}= K_{\text{accr}}\,q_\mathrm{c}\,q_\mathrm{r}\,\Phi_{\text{accr}}(\tau_\mathrm{c}) \left(\rho_0\,\rho \right)^{\frac{1}{2}}, \end{align*}$

with the accretion kernel K_accr = 4.33 m³ kg^-1 s^-1 and the similarity function

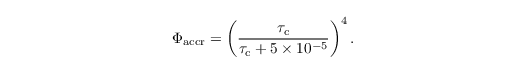
$\begin{align*} & \Phi_{\text{accr}}=\left(\frac{\tau_\mathrm{c}}{\tau_\mathrm{c} + 5 \times 10^{-5}}\right)^4. \end{align*}$

Turbulence effects on the accretion rate can be considered after using the kernel after Seifert et al. (2010).

Self-collection and breakup

Selfcollection and breakup describe merging and splitting of rain drops, respectively, which affect the rain water drop number concentration only. Their combined impact is parametrized as

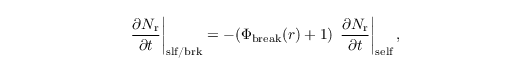
$\begin{align*} & \left.\frac{\partial N_\mathrm{r}}{\partial t} \right|_\text{slf/brk}= -(\Phi_{\text{break}}(r)+1)\,\left.\frac{\partial N_\mathrm{r}}{\partial t} \right|_{\text{self}}, \end{align*}$

with the breakup function

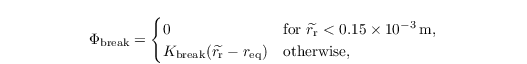
$\begin{align*} & \Phi_{\text{break}} = \begin{cases} 0 & \text{for~} \widetilde{r_\mathrm{r}} < 0.15 \times 10^{-3}\,\mathrm{m},\\ K_{\text{break}} (\widetilde{r_\mathrm{r}}-r_{\text{eq}}) & \text{otherwise}, \end{cases} \end{align*}$

depending on the volume averaged rain drop radius

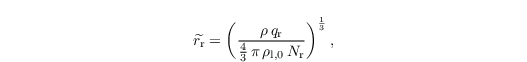
$\begin{align*} & \widetilde{r_\mathrm{r}}=\left(\frac{\rho\,q_\mathrm{r}}{\frac{4}{3}\,\pi\,\rho_{\mathrm{l},0}\,N_\mathrm{r}} \right)^{\frac{1}{3}}, \end{align*}$

the equilibrium radius r_eq = 550 x 10^-6 m and the breakup kernel K_break = 2000 m^-1. The local temporal change of N_r due to selfcollection is

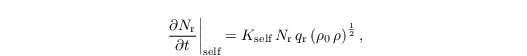
$\begin{align*} & \left.\frac{\partial N_\mathrm{r}}{\partial t} \right|_{\text{self}}= K_{\text{self}}\,N_\mathrm{r}\,q_\mathrm{r} \left(\rho_0\,\rho \right)^{\frac{1}{2}}, \end{align*}$

with the selfcollection kernel K_self = 7.12 m³ kg^-1 s^-1.

Evaporation of rainwater

The evaporation of rain drops in subsaturated air (relative water supersaturation S < 0) is parametrized following Seifert (2008):

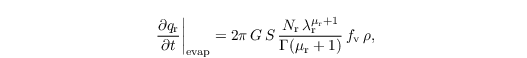
$\begin{align*} & \left.\frac{\partial q_\mathrm{r}}{\partial t} \right|_{\text{evap}}= 2 \pi\,G\,S\,\frac{N_\mathrm{r}\,\lambda_\mathrm{r}^{\mu_\mathrm{r}+1}}{\Gamma(\mu_\mathrm{r}+1)}\,f_\mathrm{v}\,\rho, \end{align*}$

where

$\begin{align*} & G = \left[\frac{R_\mathrm{v}T}{K_\mathrm{v}p_\text{v, s}(T)} + \left(\frac{L_\mathrm{V}}{R_\mathrm{v} T}-1\right) \frac{L_\mathrm{V}}{\lambda_\mathrm{h}\,T}\right]^{-1}, \end{align*}$

with K_v = 2.3 x 10^-5 m² s^-1 being the molecular diffusivity water vapor in air and λ_h = 2.43 x 10^-2 W m^-1 K^-1 being the heat conductivity of air. Here, N_r λ_r^μ_r+1 / Γ(μ_r+1) denotes the intercept parameter of the rain drop gamma distribution with Γ being the gamma-function. Following Stevens and Seifert (2008), the slope parameter reads as

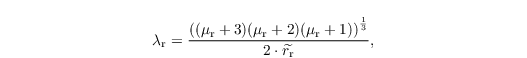
$\begin{align*} & \lambda_\mathrm{r} = \frac{\left((\mu_\mathrm{r}+3) (\mu_\mathrm{r}+2) (\mu_\mathrm{r}+1)\right)^{\frac{1}{3}}}{2 \cdot \widetilde{r_\mathrm{r}}}, \end{align*}$

with μ_r being the shape parameter, given by

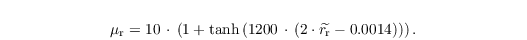
$\begin{align*} & \mu_\mathrm{r} = 10\,\cdot\,\left(1 + \tanh{\left(1200\,\cdot\,\left(2 \cdot \widetilde{r_\mathrm{r}} - 0.0014 \right)\right)} \right). \end{align*}$

In order to account for the increased evaporation of falling rain drops, the so-called ventilation effect, a ventilation factor f_v is calculated optionally by a series expansion considering the rain drop size distribution (Seifert, 2008, Appendix).

The complete evaporation of rain drops (i.e., their evaporation to a size smaller than the separation radius of 40 µm) is parametrized as

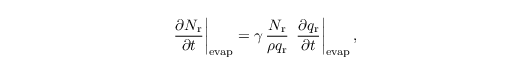
$\begin{align*} & \left.\frac{\partial N_\mathrm{r}}{\partial t} \right|_{\text{evap}}= \gamma\,\frac{N_\mathrm{r}}{\rho q_\mathrm{r}}\,\left.\frac{\partial q_\mathrm{r}}{\partial t} \right|_{\text{evap}}, \end{align*}$

with γ = 0.7 (see also Heus et al., 2010).

Sedimentation of cloudwater

As shown by Ackerman et al. (2009), the sedimentation of cloud water has to be taken in account for the simulation of stratocumulus clouds. They suggest the cloud water sedimentation flux to be calculated as

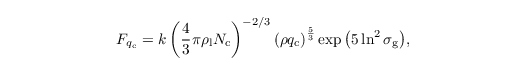
$\begin{align*} & F_{q_\mathrm{c}} = k \left(\frac{4}{3} \pi\rho_\mathrm{l}N_\mathrm{c}\right)^{-2/3} \left(\rho q_\mathrm{c}\right)^{\frac{5}{3}} \exp{\left(5 \ln^2{\sigma_\mathrm{g}}\right)}, \end{align*}$

based on a Stokes drag approximation of the terminal velocities of log-normal distributed cloud droplets. Here, k = 1.2 x 10⁸ m^-1 s^-1 is a parameter and σ_g = 1.3 the geometric SD of the cloud droplet size distribution (Geoffroy et al., 2010). The tendency of q results from the sedimentation flux divergences and reads as

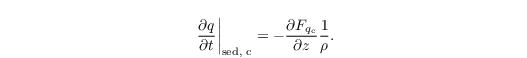
$\begin{align*} & \left.\frac{\partial q}{\partial t} \right|_\text{sed, c}= - \frac{\partial F_{q_\mathrm{c}}}{\partial z} \frac{1}{\rho}. \end{align*}$

Sedimentation of rainwater

The sedimentation of rain water is implemented following Stevens and Seifert (2008). The sedimentation velocities are based on an empirical relation for the terminal fall velocity after Rogers et al. (1993). They are given by

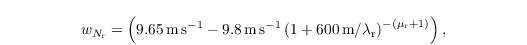
$\begin{align*} & w_{N_\mathrm{r}} = \left(9.65\,\text{m\,s}^{-1} - 9.8\,\text{m\,s}^{-1} \left(1+ 600\,\text{m}/\lambda_\mathrm{r}\right)^{-(\mu_\mathrm{r} + 1)} \right), \end{align*}$

and

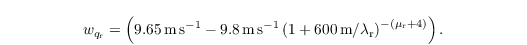
$\begin{align*} & w_{q_\mathrm{r}} = \left(9.65\,\text{m\,s}^{-1} - 9.8\,\text{m\,s}^{-1} \left(1+ 600\,\text{m}/\lambda_\mathrm{r}\right)^{-(\mu_\mathrm{r} + 4)} \right). \end{align*}$

The resulting sedimentation fluxes F_Nr and F_qr are calculated using a semi-Lagrangian scheme and a slope limiter (see Stevens and Seifert, 2008, their Appendix A). The resulting tendencies read as

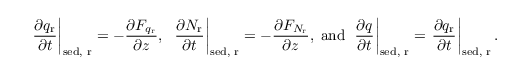
$\begin{align*} & \left.\frac{\partial q_\mathrm{r}}{\partial t} \right|_\text{sed, r}= -\frac{\partial F_{q_\mathrm{r}}}{\partial z},~ \left.\frac{\partial N_\mathrm{r}}{\partial t} \right|_\text{sed, r}= -\frac{\partial F_{N_\mathrm{r}}}{\partial z},\;\text{and}~ \left.\frac{\partial q}{\partial t} \right|_\text{sed, r}= \left.\frac{\partial q_\mathrm{r}}{\partial t} \right|_\text{sed, r}. \end{align*}$

Turbulence closure

Using bulk cloud microphysics, PALM predicts liquid water temperature θ_l and total water mixing ratio q instead of θ and q_v. Consequently, some terms in the Eq. for

$\overline{w^{\prime\prime}{\theta_{\mathrm{v}}}^{\prime\prime}}$

of Sect. turbulence closure are unknown. We thus follow Cuijpers and Duynkerke (1993) and calculate the SGS buoyancy flux from the known SGS fluxes

$\overline{w^{\prime\prime}{\theta_{\mathrm{l}}}^{\prime\prime}}$

and

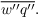
$$\overline{w^{\prime\prime}{q}^{\prime\prime}}$.$

In unsaturated air (q_c = 0) the Eq. for

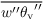
$\overline{w^{\prime\prime} {\theta_{\mathrm{v}}}^{\prime\prime}}$

of Sect. turbulence closure is then replaced by

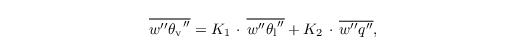
$\begin{align*} & \overline{w^{\prime\prime} {\theta_{\mathrm{v}}}^{\prime\prime}}=K_1\,\cdot\,\overline{w^{\prime\prime} {\theta_\mathrm{l}}^{\prime\prime}} + K_2\,\cdot\,\overline{w^{\prime\prime} {q}^{\prime\prime}}, \end{align*}$

with

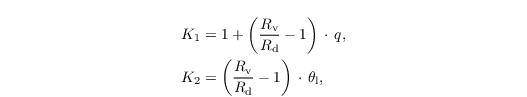
$\begin{align*} & K_1 = 1+\left(\frac{R_\mathrm{v}}{R_\mathrm{d}}-1\right)\,\cdot\,q,\\ & K_2 = \left(\frac{R_\mathrm{v}}{R_\mathrm{d}}-1\right)\,\cdot\,\theta_\mathrm{l}, \end{align*}$

and in saturated air (q_c > 0) by

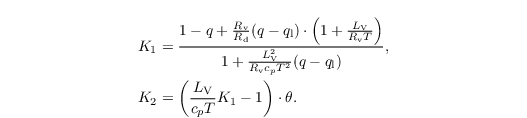
$\begin{align*} & K_1 =\frac{1 - q + \frac{R_\mathrm{v}}{R_\mathrm{d}} (q-q_\mathrm{l}) \cdot \left(1 + \frac{L_\mathrm{V}}{R_\mathrm{v} T} \right)}{1 + \frac{L_\mathrm{V}^2}{R_\mathrm{v} c_p T^2} (q-q_\mathrm{l})},\\ & K_2 = \left(\frac{L_\mathrm{V}}{c_p T} K_1 - 1 \right) \cdot \theta. \end{align*}$

Recent applications

The two-moment cloud microphysics scheme has been used within the framework of the HD(CP)² (High Definition Clouds and Precipitation for Climate Prediction, http://www.hdcp2.eu) project to produce LES simulation data for the evaluation and benchmarking of ICON-LES (Dipankar et al., 2015). Figure 8 contains a snapshot from such a benchmark simulation, where three continuous days were simulated. The figure shows the simulated clouds including precipitation events on 26 April 2013 during a frontal passage. Moreover, cloud microphysics have been recently used for investigations of shadow effects of shallow convective clouds on the ABL and their feedback on the cloud field (Gronemeier et al. 2016).

Figure 8: Snapshot of the cloud field from a PALM run for three continuous days of the HD(CP)² Observational Prototype Experiment. Shown is the 3-D field of q_c (white to gray colors) as well as rain water (q_r > 0, blue) on 26 April 2013. The simulation had a grid-spacing of 50 m on a 50 x 50 km² domain. Large-scale advective tendencies for θ_l and q were taken from COSMOE-DE (regional model of German Meteorological Service, DWD) analyses. The copyright for the underlying satellite image is held by Cnes / Spot Image, Digitalglobe.

References

Arnason G, Brown J. 1971. Growth of cloud droplets by condensation: A problem in computational stability. J. Atmos. Sci. 28: 72-77.

Emanuel KA. 1994. Atmospheric Convection. Oxford University Press.

Seifert A, Beheng KD. 2001. A double-moment parameterization for simulating autoconversion, accretion and selfcollection. Atmos. Res. 59: 265–281.

Seifert A, Beheng KD. 2006. A two-moment cloud microphysics parameterization for mixed-phase clouds. Part 1: Model description. Meteorol. Atmos. Phys. 92: 45–66.

Savic-Jovcic V, Stevens B. 2008. The structure and mesoscale organization of precipitating stratocumulus. J. Atmos. Sci. 65: 1587–1605. doi

Heus T, van Heerwaarden CC, Jonker HJJ, Pier Siebesma A, Axelsen S, van den Dries K, Geoffroy O, Moene AF, Pino D, de Roode SR, Vilà-Guerau de Arellano J. 2010. Formulation of the Dutch Atmospheric Large-Eddy Simulation (DALES) and overview of its applications. Geosci. Model Dev. 3: 415–444. doi

Stevens B, Seifert A. 2008. Understanding macrophysical outcomes of microphysical choices in simulations of shallow cumulus convection. J. Meteor. Soc. Jpn. 86: 143–162.

Bougeault, P. 1981. Modeling the trade-wind cumulus boundary layer. Part I: Testing the ensemble cloud relations against numerical data. J. Atmos. Sci. 38: 2414–2428.

Khairoutdinov M, Kogan Y. 2000. A new cloud physics parameterization in a large-eddy simulation model of marine stratocumulus. Mon. Weat. Rev. 128: 229–243.

Sommeria G, Deardorff JW. 1977. Subgrid-scale condensation in models of nonprecipitating clouds. J. Atmos. Sci. 34: 344–355.

Kessler E. 1969. On the Distribution and Continuity of Water Substance in Atmospheric Circulation. Meteor. Monogr: 1-84.

Pruppacher HR, and Klett JD. 1997. Microphysics of Clouds and Precipitation. 2nd Edn. Kluwer Academic Publishers. Dordrecht.

Morrison H. 2007. Comparison of bulk and bin warm-rain microphysics models using a kinematic framework. J. Atmos. Sci. 64: 2839-2681.

Seifert A, Nuijens L, Stevens B. 2010. Turbulence effects on warm-rain autoconversion in precipitating shallow convection. Q. J. Roy. Meteor. Soc. 136: 1753–1762.

Seifert A. 2008. On the parameterization of evaporation of raindrops as simulated by a one-dimensional rainshaft model. J. Atmos. Sci. 65: 3608–3619. doi.

Ackerman, AS, vanZanten MC, Stevens B, Savic-Jovcic V, Bretherton CS, Chlond A, Golaz J-C, Jiang H, Khairoutdinov M, Krueger SK, Lewellen DC, Lock A, Moeng C-H, Nakamura K, Petters MD, Snider JR, Weinbrecht S, Zuluaf M. 2009. Large-eddy simulations of a drizzling, stratocumulus-topped marine boundary layer, Mon. Weather Rev., 137: 1083–1110.

Geoffroy O, Brenguier J-L, Burnet F. 2010. Parametric representation of the cloud droplet spectra for LES warm bulk microphysical schemes. Atmos. Chem. Phys. 10: 4835–4848. doi.

Rogers RR, Baumgardner D, Ethier SA, Carter DA, Ecklund WL. 1993. Comparison of raindrop size distributions measured by radar wind profiler and by airplane. J. Appl. Meteorol. 32: 694–699.

Cuijpers JWM, Duynkerke PG. 1993. Large eddy simulation of trade wind cumulus clouds. J. Atmos. Sci. 50: 3894–3908.

Dipankar A, Stevens B, Heinze R, Moseley C, Zängl G, Giorgetta M, Brdar D. 2015. Large eddy simulation using the general circulation model ICON. J. Adv. Mod. Earth Syst. 07. doi.

Gronemeier T, Kanani-Sühring F, Raasch S. 2016. Do shallow cumulus clouds have the potential to trigger secondary circulations via shading? Boundary-Layer Meteorol. doi.

Attachments (8)

Table4.png (114.2 KB) - added by Giersch 9 years ago. List of cloud physics parameters and symbols
Table5.png (38.6 KB) - added by Giersch 9 years ago. List of LPM symbols and parameters
Table6.png (32.0 KB) - added by Giersch 9 years ago. List of canopy model parameters and symbols
06.png (3.0 MB) - added by Giersch 8 years ago. Snapshot of the cloud field from a PALM run for.
Button_Example.png (56.3 KB) - added by westbrink 6 years ago.
Button_InputPara.png (57.8 KB) - added by westbrink 6 years ago.
Button_Overview.png (56.0 KB) - added by westbrink 6 years ago.
Button_References.png (55.5 KB) - added by westbrink 6 years ago.

Download in other formats:

Plain Text