Home


About us
PALM
PALM-4U
Installation
Release notes
Documentation
Getting Help
Gallery
Developers area

Version 8 (modified by kanani, 6 years ago) (diff)

--

Pressure solver

The Boussinesq approximation requires incompressibility of the flow, but the integration of the governing equations formulated in Sect. governing equations does not provide this feature. Divergence of the flow field is thus inherently produced. Hence, a predictor corrector method is used where an equation is solved for the modified perturbation pressure after every time step (e.g., Patrinos and Kistler, 1977). In a first step, the pressure term

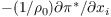
$ -(1/\rho_0) \partial \pi^\ast/\partial x_i $

is excluded from the first Equation in Sect. governing equations during time integration. This yields a preliminary velocity ui.pret+Δt at time t + Δt. Emerging divergences can then be attributed to the pressure term. Subsequently, the prognostic velocity can be decomposed in a second step as

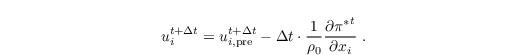
\begin{align*} & u_{i}^{t+\Delta t} = u_{i,\text{pre}}^{t+\Delta t} - \Delta t \cdot \frac{1}{\rho_0} \frac{\partial {\pi^\ast}^t}{\partial x_i}\;. \end{align*}

The third step then is to stipulate incompressibility for uit+Δt:

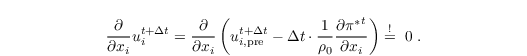
\begin{align*} & \frac{\partial}{\partial x_i} u_{i}^{t+\Delta t} = \frac{\partial}{\partial x_i}\left(u_{i,\text{pre}}^{t+\Delta t} - \Delta t \cdot \frac{1}{\rho_0} \frac{\partial {\pi^\ast}^t}{\partial x_i}\right) \overset{!}{=}~ 0\;. \end{align*}

The result is a Poisson equation for π∗:

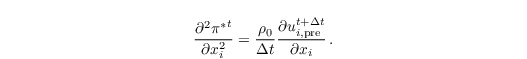
\begin{align*} & \frac{\partial^2 {\pi^\ast}^t}{\partial x_i^2} = \frac{\rho_0}{\Delta t} \frac{\partial u_{i,\text{pre}}^{t+\Delta t}}{\partial x_i}\,. \end{align*}

The exact solution of that Equation would give a π∗ that yields a uit+Δt free of divergence when used in the first equation mentioned above. In practice, a numerically efficient reduction of divergence by several orders of magnitude is found to be sufficient. Note that the differentials in the equation above are used for convenience and that the model code uses finite differences instead. When employing a Runge Kutta time stepping scheme, the formulation above is used to solve the Poisson equation for each substep. π∗ is then calculated from its weighted average over these substeps.

In case of cyclic lateral boundary conditions, the solution of the Poisson equation is achieved by using a direct fast Fourier transform (FFT). The Poisson equation is Fourier transformed in both horizontal directions, the resulting tri-diagonal matrix is solved along the "z" direction, and then transformed back (see, e.g., Schumann and Sweet, 1988). PALM provides the inefficient but less restrictive Singleton-FFT (Singleton, 1969) and the well optimized Temperton-FFT (Temperton, 1992). External FFT libraries can be used as well, with the FFTW (Frigo and Johnson, 1998) being the most efficient one. Alternatively, the iterative multigrid scheme can be used (e.g., Hackbusch, 1985). This scheme uses the Gauss–Seidel method for the inner iterations on each grid level. The convergence of this scheme is steered by the number of so-called V- or W-cycles to be carried out for each call of the scheme and by the number of Gauss–Seidel iterations to be carried out on each grid level. As the multigrid scheme does not require periodicity along the horizontal directions, it allows for using non-cyclic lateral boundary conditions.

References

  • Patrinos ANA, Kistler AL. 1977. A numerical study of the Chicago lake breeze. Bound.-Lay. Meteorol. 12: 93–123.
  • Schumann U, Sweet RA. 1988. Fast Fourier Transforms for Direct Solution of Poisson's Equation with Staggered Boundary Conditions. J. Comput. Phys. 75: 123–137.
  • Singleton RC. 1969. An algorithm for computing the mixed radix fast Fourier transform. IEEE T. Acoust. Speech. 17: 93–103.
  • Temperton C. 1992. A Generalized Prime Factor FFT Algorithm for Any N =2p 3q 5r. SIAM J. Sci. Stat. Comp. 13: 676–686.
  • Frigo M, Johnson SG. 1998. FFTW: an adaptive software architecture for the FFT. in: Proc. of the 1998 IEEE International Conference on Acoustics, Speech and Signal Processing. 381–1384.
  • Hackbusch W. 1985. Multigrid Methods and Applications. Springer. Berlin, Heidelberg, New York. 378 pp.
                                                                                                                                                                                                                                                                                                                                                                               
  | Impressum | ©Leibniz Universität Hannover |