Particle code structure

This section will give a brief summary of the particle code structure and the changes carried out for PALM 4.0. These changes are aiming at reaching a significantly improved performance of the LPM in comparison to the previous versions described by Steinfeld et al. (2008) and Riechelmann et al. (2012).

Each particle is defined by its features, which are stored as components of a Fortran 95 derived data type (e.g., Metcalf et al., Chap.~2.9):

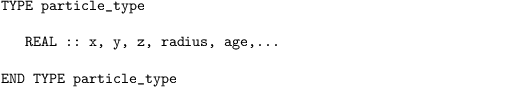
Here, x, y, z, radius and age are some components of the derived data type of the intrinsic data type REAL. Several other components of all intrinsic data types (or even other derived data types) can be defined (e.g., location, velocity). In general, the particles are stored in an allocatable array of the derived data type

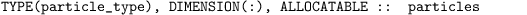
An element of particles defines a complete particle with its entire features, which can be accessed by the selector %, e.g., the radius and age of the particles by

and

respectively, where n is the index of a certain particle. In the old PALM version, all particles of the respective subdomain were stored in such a 1-D array.

Since many quantities derived from the LPM depend solely on the particles located in a certain grid volume, e.g., the collision and coalescence process of the LCM (see Sect. collision and coalescence, the order in which these particles are stored in memory determines heavily the CPU time for the LPM. In general, N² operations, where N is the number of all simulated particles, are needed to identify the particles located in the vicinity of another particle (see Riechelmann et al., 2012). In the previous versions of the LPM, this amount of operations was reduced to N by sorting the particles according to the grid volumes in which they are located. However, due to the large number of about 10⁶ particles stored, sorting was inefficient and also demanded a temporary array of the same size during sorting.

Therefore, from PALM 4.0 on, all particles are stored in a new array-structure based on another derived data type named particle_grid_type, which contains, as a component, a 1-D array of the derived data type particle_type:

Note that the individual particle features are still accessible as components of particles. An allocatable three-dimensional array of particle_grid_type is defined

and allocated using the same dimensions as used for a scalar of the LES model. In this way, all particles currently located in a certain LES grid volume are permanently stored in the particle array, assigned to this grid volume:

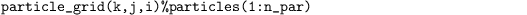
Here, n_par is the number of particles located in the grid volume defined by the indices k, j, and i. The small size of this particle array at each grid volume (typically containing roughly 10² particles) allows the de-allocation and allocation of the particle array during the simulation adapting its size to the number of required particles. This was (practically) not possible in the previous version of the LPM due to the large size of the full particle array (about 10⁶ particles), which required a temporary array of the same size during re-allocation. A temporary array is still required in the present version, but its size could be reduced by four orders of magnitude. However, as a particle moves from one grid volume to another, its data has to be copied from the 1-D array of the previous grid volume to the 1-D array of the new volume, and finally deleted from previous one, which consumes CPU time itself. Overall, the new particle structure reduces the CPU time of the LPM by 9 %, since sorting of particles is not required anymore. Moreover, large temporary arrays are no longer required, which increases the available memory by almost a~factor of two (which doubles the hypothetical amount of allocatable particles for future studies).

From PALM 4.0 on, the LPM features an optimized version of the tri-linear interpolation of LES data fields on the location of the particle. In general, the particles located in a certain grid volume are stored in an arbitrary order. Because of the staggered grid, indices of the eight surrounding grid points required for interpolation may differ from particle to particle (e.g., a particle in the lower left corner of a scalar grid box requires other data for interpolation than a particle in the upper right corner). This would require to re-calculate the respective index values for every new particle. By dividing every grid volume in eight subgrid boxes, two in every spatial direction, the same set of LES data can be used for all particles located in the same subgrid box (see example in Fig. 14 at the end off this Sect.). Therefore, the particles belonging to the same subgrid box are stored contiguously in memory reducing the CPU time substantially for the different subroutines depending on the interpolation of LES fields substantially (e.g., advection by 64 %, condensational growth by 50 %, whole LPM by 22 %), whereas the time needed for additional sorting increases the CPU time by only 3 %.

In summary, these optimizations reduce the CPU time of the LPM by 40 % and almost halve its memory demand. For simulations with hundreds of millions of particles, the LPM consumes more than 95 % of the overall CPU time of PALM and the memory demand of the particles is the limiting factor for these simulations (see high-end applications, e.g., Riechelmann et al., 2012; Lee et al., 2014; Sühring et al., 2015). The present version of the LPM now allows for larger amounts of particles.

Figure 14: Two-dimensional example of the optimized interpolation algorithm. Interpolating a scalar quantity (e.g., temperature) bi-linearly on a particle (blue dot) located in a certain LES grid box (thick black line) includes four values of LES-data (red squares). Note that these values are the same for all particles located in the yellow subgrid box. Thus, by sorting all particles inside a grid box by their respective subgrid box, the indices required for interpolation need to be determined just once for all particles located in that subgrid box, and not repeatedly for all particle inside the entire grid box. This algorithm applies analogously for the velocity components located at the edges of the grid box.

References

• Steinfeld G, Raasch S, Markkanen T. 2008. Footprints in homogeneously and heterogeneously driven boundary layers derived from a Lagrangian stochastic particle model embedded into large-eddy simulation. Bound.-Lay. Meteorol. 129: 225–248.

• Riechelmann T, Noh Y, Raasch S. 2012. A new method for large-eddy simulations of clouds with Lagrangian droplets including the effects of turbulent collision. New J. Phys. 14: 065008. ​doi.

• Metcalf M, Reid JK, Cohen M. 2004. Fortran 95/2003 Explained. vol. 416. Oxford University Press. Oxford.

• Lee JH, Noh Y, Raasch S, Riechelmann T, Wang L-P. 2014. Investigation of droplet dynamics in a convective cloud using a Lagrangian cloud model. Meteorol. Atmos. Phys. 124: 1–21. ​doi.

• Sühring M, Kanani F, Charuchittipan D, Foken T, Raasch S. 2015. Footprint estimation for elevated turbulence measurements - a comparison between large-eddy simulation and a Lagrangian stochastic backward model. Bound.-Lay. Meteorol. under revision.