Home

Context Navigation

Version 2 (modified by sward, 6 years ago) (diff)
--

Social Forces

TracNav

Multi Agent System

This page is part of the Multi Agent System documentation.
It contains a description of the Social Forces approach for pedestrian interactions used in this module.
For an overview of all MAS-related pages, see the MAS main page.

Agent movement and close-range interaction is implemented using a modified Social Force Model. The implementation uses concepts from the original Social Force Model (Helbing, 1995) and an extension of it for close-rage collision prediction and avoidance (Karamouzas et. al, 2014).
The Social Forces approach is based on the idea that pedestrian movement is results from forces exerted on the pedestrian by its surroundings and goals. These forces can be either repulsive or attractive. Repulsive forces are associated with obstacles such as buildings, trees or other pedestrians. The current goal of each pedestrian exerts an attractive force on it. The resulting force on a pedestrian α is the sum of all attractive and repulsive forces,

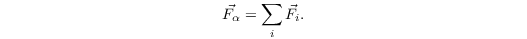
$\begin{equation*} \vec{F_{\alpha}} = \sum_i{\vec{F_i}}. \end{equation*}$

The forces considered here are repulsion by obstacles and other pedestrians as well as the acceleration term driving the pedestrian toward its target.

The repulsion by an obstacle B is defined as

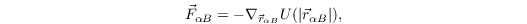
$\begin{equation*} \vec{F}_{\alpha B} = - \nabla_{\vec{r}_{\alpha B}} U(|\vec{r}_{\alpha B}|), \end{equation*}$

with the repulsive potential

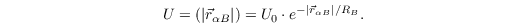
$\begin{equation*} U = (|\vec{r}_{\alpha B}|) = U_0 \cdot e^{-|\vec{r}_{\alpha B}|/R_{B}}. \end{equation*}$

In the MAS, U₀ is repuls_wall and R_B is sigma_rep_wall.

The repulsion by another pedestrian β is defined as

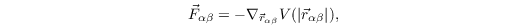
$\begin{equation*} \vec{F}_{\alpha \beta} = - \nabla_{\vec{r}_{\alpha \beta}} V(|\vec{r}_{\alpha \beta}|), \end{equation*}$

with the repulsive potential

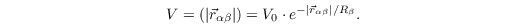
$\begin{equation*} V = (|\vec{r}_{\alpha \beta}|) = V_0 \cdot e^{-|\vec{r}_{\alpha \beta}|/R_{\beta}}. \end{equation*}$

In the MAS, V₀ is repuls_agent and R_β is sigma_rep_agent. This agent repulsive force is only used if α and β are already colliding (i.e. two circles with centers at the respective agents' position with radius radius_agent are intersecting). Otherwise, a collision avoidance force according to (Karamouzas et. al, 2014) is calculated:

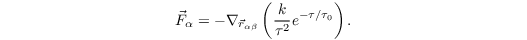
$\begin{equation*} \vec{F}_{\alpha} = -\nabla_{\vec{r}_{\alpha \beta}} \left( \frac{k}{\tau^2}e^{-\tau/\tau_0} \right). \end{equation*}$

Here, τ is the time until, given the current trajectory, a collision between the two pedestrians would occur, τ₀ = 3 s and k is a constant to sets the units with a value of 1.5 m² kg.

The acceleration force

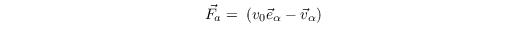
$\begin{equation*} \vec{F_a} = \frac{}{}(v_0\vec{e}_{\alpha} - \vec{v}_{\alpha}) \end{equation*}$

describes the tendency of a pedestrian to accelerate toward its target. Here, τ_α is a relaxation time (tau_accel_agent) that describes how quickly the pedestrian approaches v₀ its desired walking speed with the direction to its current target, e.

The pedestrian's walking speed is given by

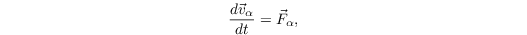
$\begin{equation*} \frac{d\vec{v}_{\alpha}}{dt} = \vec{F}_{\alpha}, \end{equation*}$

with a simple Euler-forward method used for time-integration.

Examples

For an example job to get to know the MAS, have a look at
trunk/EXAMPLES/agents

References

Helbing, D., Molnar, P. (1995). Social force model for pedestrian dynamics. Physical review E, 51(5), 4282. doi
Karamouzas, I., Skinner, B., Guy, S.J. 2014. Universal Power Law Governing Pedestrian Interactions. Pyhsical Review Letters, 113, 238701. doi

Download in other formats:

Plain Text