Home

Context Navigation

1-D model for precursor runs

The initial profiles of the horizontal wind components in PALM can be prescribed by the user by piecewise linear gradients or by directly using observational data. Alternatively, a 1-D model can be employed to calculate stationary boundary-layer wind profiles. This is particularly useful in neutral stratification, where inertial oscillations can persist for several days in case that non-balanced profiles are used for initialization. By employing the embedded computationally inexpensive 1-D model with a Reynolds-average based turbulence parametrization, these oscillations can be significantly damped. A stationary state of the wind profiles can thus be provided much faster in the 3-D model. The arrays of the 3-D variables are then initialized with the (stationary) solution of the 1-D model. These variables are u_i where i ∈ {1, 2}, e, K_h, K_m and, with MOST applied between the surface and the first vertical grid level, also L, u_∗ as well as

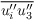
$\overline{u_i^{\prime\prime} u_3^{\prime\prime}}$

(where i ∈ {1, 2}).

The 1-D model assumes the profiles of θ and q_v, as prescribed by the user, to be constant in time. The model solves the prognostic equations for u_i and e:

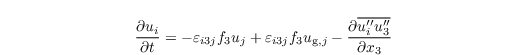
$\begin{align*} & \frac{\partial u_i}{\partial t} = -\varepsilon_{i3j}f_3 u_j + \varepsilon_{i3j}f_3 {u_{\mathrm{g},j}} - \frac{\partial \overline{u_i^{\prime\prime}u_3^{\prime\prime}}}{\partial x_3} \end{align*}$

and

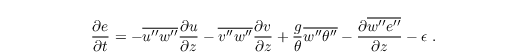
$\begin{align*} & \frac{\partial e}{\partial t} = - \overline{u^{\prime\prime}w^{\prime\prime}} \frac{\partial u}{\partial z} - \overline{v^{\prime\prime}w^{\prime\prime}} \frac{\partial v}{\partial z} + \frac{g}{\theta} \overline{w^{\prime\prime}\theta^{\prime\prime}} - \frac{\partial \overline{w^{\prime\prime}e^{\prime\prime}}}{\partial z} - \epsilon\;. \end{align*}$

The dissipation rate is parametrized by

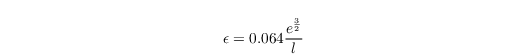
$\begin{align*} & \epsilon = 0.064 \frac{e^{\frac{3}{2}}}{l} \end{align*}$

after Detering and Etling (1985). The mixing length is calculated after Blackadar (1997) as

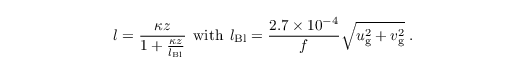
$\begin{align*} & l = \frac{\kappa z}{1 + \frac{\kappa z}{l_{\text{Bl}}}}\,\;\text{with}\,\;l_{\text{Bl}} = \frac{2.7\times10^{-4}}{f}\sqrt{u_{\mathrm{g}}^2 + v_{\mathrm{g}}^2}\;. \end{align*}$

The turbulent fluxes are calculated using a 1st-order closure:

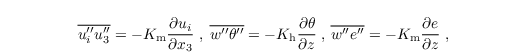
$\begin{align*} & \overline{u_i^{\prime\prime}u_3^{\prime\prime}} = - K_\mathrm{m} \frac{\partial u_i}{\partial x_3}\;,\;\overline{w^{\prime\prime}\theta^{\prime\prime}} = - K_\mathrm{h} \frac{\partial \theta}{\partial z} \;,\,\overline{w^{\prime\prime}e^{\prime\prime}} = - K_\mathrm{m} \frac{\partial e}{\partial z}\;, \end{align*}$

where K_m and K_h are calculated as

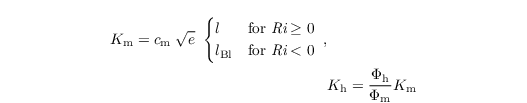
$\begin{align*} K_\mathrm{m} = c_\mathrm{m}\;\sqrt{e}\ \begin{cases} l & \text{for~} \textit{Ri} \geq 0\\ l_{\text{Bl}} & \text{for~} \textit{Ri} < 0\\ \end{cases}\;,\\ &K_\mathrm{h} = \frac{\Phi_\mathrm{h}}{\Phi_\mathrm{m}} K_\mathrm{m} \end{align*}$

with the similarity functions Φ_h and Φ_m (see Eqs. in Sect boundary conditions), using the gradient Richardson number:

$\begin{align*} & \textit{Ri} = \frac{\frac{g}{\theta_\mathrm{v}}\frac{\partial\theta}{\partial z}}{\left[\left(\frac{\partial u}{\partial z}\right)^2 + \left(\frac{\partial v}{\partial z}\right)^2 \right]} \cdot \begin{cases} 1\,\;&\text{for~}\,\;\textit{Ri} \geq 0\;,\\ (1 - 16 \cdot \textit{Ri})^{\frac{1}{4}}\,\;&\text{for~}\,\;\textit{Ri} < 0\;. \end{cases} \end{align*}$

Note that the distinction of cases in the Eq. above is done with the value of Ri from the previous time step.

Moreover, a Rayleigh damping can be switched on to speed up the damping of inertial oscillations. The 1-D model is discretized in space using finite differences. Discretization in time is achieved using the 3rd-order Runge--Kutta time-stepping scheme (Williamson, 1980). Dirichlet boundary conditions are used at the top and bottom boundaries of the model, except for e, for which Neumann conditions are set at the surface (see also Sect. boundary conditions).

References

Detering HW, Etling D. 1985. Application of the E-ε turbulence model to the atmospheric boundary layer. Bound.-Lay. Meteorol. 33: 113–133.

Blackadar AK. 1997. Turbulence and Diffusion in the Atmosphere. Springer. Berlin. Heidelberg. NewYork?. 185 pp.

Williamson JH. 1980. Low-storage Runge–Kutta schemes. J. Comput. Phys. 35: 48–56.

Last modified 7 years ago Last modified on Aug 2, 2017 9:53:51 AM

Download in other formats:

Plain Text