Home

Context Navigation

Version 20 (modified by boeske, 9 years ago) (diff)
--

Non-cyclic lateral boundary conditions

Figure 1 shows the grid structure for non-cyclic boundary conditions at the left/right boundary LB/RB (bc_lr) and figure 2 for non-cyclic boundary conditions at the north/south boundary NB/SB (bc_ns). The indices (i,j,k) represent the directions (x,y,z). The model domain extends from -1:nx+1 in the x-direction, from -1:ny+1 in the y-direction and from 0:nzt+1 in the z-direction. For the advection scheme of Wicker and Skamarock, two more grid points are added at the lateral boundaries which are not needed for non-cyclic boundary conditions. The figures display the grid layer of the horizontal velocity components u and v, and scalar s. The grid points of the vertical velocity w are defined at the scalar position but shifted by one half grid spacing in vertical direction (not shown, detailed information about the grid structure in PALM can be found here). The prognostic equations are solved at all inner grid points which are marked black. The grid points at the respective non-cyclic boundaries (blue) are treated as follows.

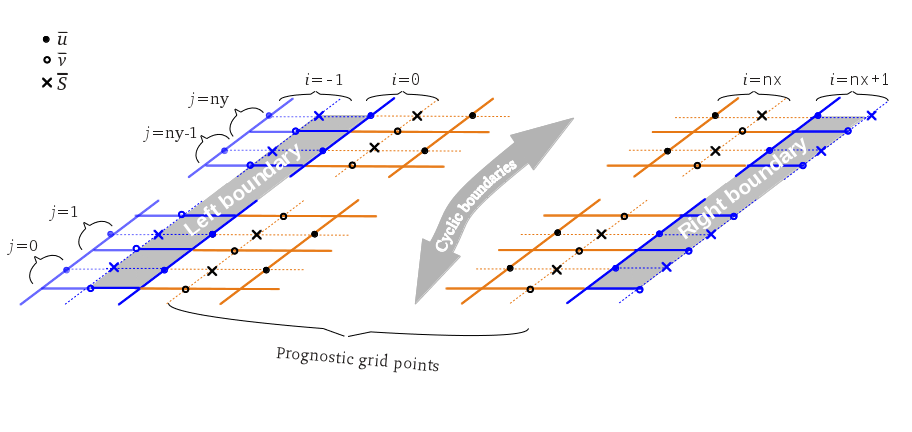
Figure 1: Grid structure at the lateral boundaries with non-cyclic lateral boundary conditions along the left-right direction.

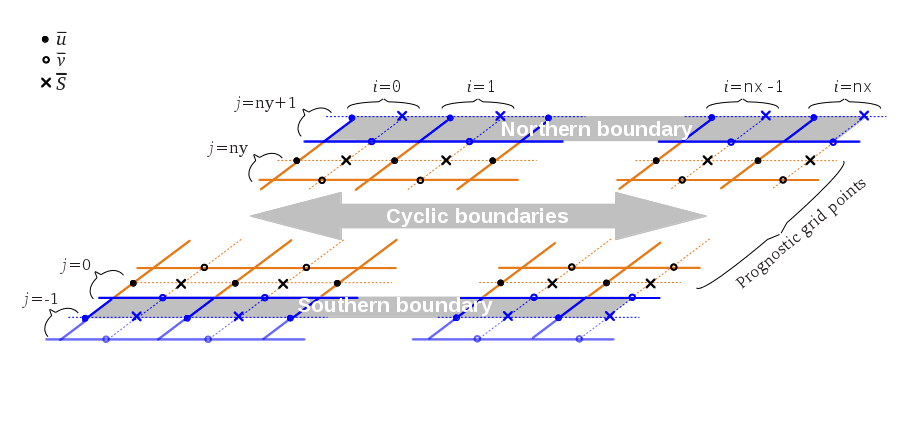
Figure 2: Grid structure of the lateral boundaries with non-cyclic lateral boundary conditions along the north-south direction.

LB is defined at i = -1 for v, w, s and at i = 0 for u. SB is defined at j = -1 for u, w, s and at j = 0 for v. RB is defined at i = nx + 1 and NB at j = ny + 1 for all quantities. LB and SB are treated this way so that the order and number of grid points for the streamwise velocity component and scalars is the same, independent of the flow direction.
For technical reasons, the prognostic equations are first solved for u at i = 0 (v at j = 0), since these grid points technically belong to the inner grid, but afterwards, these results at i = 0 (j = 0) are replaced by the respective boundary condition in routine boundary_conds.f90. In case of a Dirichlet condition, the values at i = 0 (j = 0) are taken from i = -1 (j = -1). In case of a radiation boundary condition, the solution of the Sommerfeld equation overwrites the prognostic values at i = 0 (j = 0).
For non-cyclic lateral boundary conditions, the parameter psolver has to be set to 'multigrid' because the default FFT-solver can only be applied for cyclic boundary conditions.

Inflow boundary

At the inflow boundary, Dirichlet conditions are used for the three velocity components ψ = {u,v,w} as well as for all scalar quantities s and are implemented as follows (here e.g. for s and a flow in positive x direction):

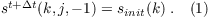
$s^{t + \Delta t}(k,j,-1) = s_{init}(k) \; . \quad(1)$

t denotes the time, Δt the time step and s_init the initialization profile of the scalar quantities which is constant in time. The quantities at the inflow are set by the initial vertical profiles (see initializing_actions). A Neumann condition is used for the subgrid-scale turbulent kinetic energy e (here e.g. for a left-right flow):

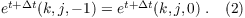
$e^{t + \Delta t}(k,j,-1) = e^{t + \Delta t}(k,j,0) \; . \quad(2)$

To prevent gravity waves from being reflected at the inflow, a relaxation term can be added to the prognostic equations for the potential temperature θ (Davies, 1976):

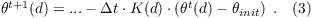
$\theta^{t+1}(d) = ... - \Delta t \cdot K(d) \cdot \left( \theta^{t}(d) - \theta_{init} \right) \; . \quad(3)$

Here, d is the distance normal to the wall and θ_init the initial value of the potential temperature, which corresponds to the value at the inflow boundary. The damping or relaxation function K depends only on the distance d to the inflow. K is calculated by

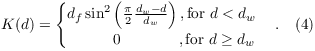
$K(d) = \begin{cases} d_f \sin^2\left( \frac{\pi}{2} \frac{d_w - d}{d_w} \right) , \text{for } d < d_w \\ \qquad\quad 0 \qquad \quad \;\;\; , \text{for } d \ge d_w \end{cases} . \quad (4)$

d_f is a damping factor to control the damping intensity, and d_w is the width of the relaxation region extending from the inflow. Quantities d_f and d_w can be set with parameters pt_damping_factor and pt_damping_width, respectively. Both parameters have to be set by the user and must be adjusted case-by-case, because both parameters depend on the numerical and physical conditions, so that application of universal default values is not possible. So far, we have experience with gravity waves in case of cold air outbreaks, which grow in amplitude up to quite extreme values, if no damping is applied. In the respective simulations, we used typical values for pt_damping_factor of 0.05 and for pt_damping_width of 25 km in order to prevent the gravity waves from growing.

Outflow boundary

At the outflow, an open boundary condition is needed to ensure that disturbances of the mean flow can exit the model domain without effecting the flow upstream. For the scalar quantities, Neumann boundary conditions are used at the outflow boundary which is the simplest way. For the velocity components, a Neumann condition would require to be considered in the solution of the Poisson equation for perturbation pressure, which has not been realized so far, because it requires some technical effort. Instead, PALM offers two types of radiation boundary conditions for the velocity components, which are not in conflict with the pressure solver (see use_cmax, bc_lr and bc_ns). For the radiation condition, the Sommerfeld radiation equation is solved at the outflow

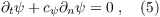
$\partial_t \psi + c_{\psi} \partial_n \psi = 0 \; , \quad (5)$

which considers flow disturbances propagating with the mean flow and by waves. Here ψ is the transported quantity and ∂_n is the derivative normal to the outflow boundary. In PALM, based on (5), the radiation boundary condition is realized in two ways as follows.

Variable Phase velocity

The phase velocity c_ψ (also called convective velocity) is calculated after Orlanski (1976):

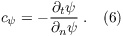
$c_{\psi} = - \dfrac{\partial_t \psi}{\partial_n \psi} \; . \quad (6)$

Left-right flow

If the outflow is defined at the right boundary (i = nx + 1, see Fig. 1), the phase velocity for each velocity components is calculated by

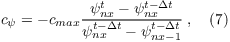
$c_{\psi} = - c_{max} \dfrac{\psi^t_{nx} - \psi^{t - \Delta t}_{nx} }{ \psi^{t-\Delta t}_{nx} - \psi^{t - \Delta t}_{nx-1} } \; , \quad (7)$

with the maximum phase velocity

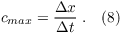
$c_{max} = \dfrac{\Delta x}{\Delta t} \; . \quad (8)$

The phase velocity has to be in the range of 0 ≤ c_ψ < c_max because negative values propagate waves back to the inner domain. c_max represents the maximum phase velocity that ensures numerical stability (Courant-Friedrichs-Lewy condition). Both conditions are not ensured by (7), hence c_ψ is set to zero for negative values and to c_max for larger values than c_max. The velocity components ψ at the outflow boundary are then calculated by

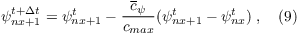
$\psi^{t+\Delta t}_{nx+1} = \psi^{t}_{nx+1} - \dfrac{\overline{c}_{\psi}}{c_{max}} (\psi^{t}_{nx+1} - \psi^{t}_{nx}) \; , \quad (9)$

with the phase velocity averaged parallel to the outflow:

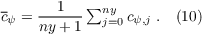
$\overline{c}_{\psi} = \dfrac{1}{ny+1} \sum_{j=0}^{ny} c_{\psi, j} \; . \quad (10)$

In Orlanskis work, the phase velocity c_ψ was not averaged along the outflow, which is sufficient for simplified flows as shown by Yoshida and Watanabe (2010). However, we found that in simulations of shear driven convective boundary layer with a strong wind component along the outflow, the approach of Orlanski (1976) was unstable. Raymond and Kuo (1984) argued that locally calculated phase velocities leads to a large variation of phase speeds which can lead to numerical instabilities. Other works used a constant phase velocity or an average over the whole outflow area (see e.g. Fröhlich 2006, p.216) instead of the approach of Orlanski (1976). With this in mind, we tested the average phase velocity calculated from (10), and the solution at the outflow becomes stable. We did not additionally average the phase velocity along the vertical direction, because the background wind usually varies with height.

For the other flow directions, the indices of equations (7)-(10) have to be replaced as follows:

$\begin{tabular}{|c |c |c |c| c|} \hline & Right-left flow &\multicolumn{2}{c|}{ South-north flow} & North-south flow \\ \hline & $(nx + 1) \rightarrow 0$ & $(nx + 1) \rightarrow -1$ & & \\ $\psi = u$ & $nx \rightarrow 1$ & $nx \rightarrow 0$ & &\\ & $(nx - 1) \rightarrow 2$ & $(nx - 1) \rightarrow 1$ & & \\ \cline{1-3} & $(nx + 1) \rightarrow -1$ & $(nx + 1) \rightarrow 0$ & & $i \rightarrow j$ \\ $\psi = v$ & $nx \rightarrow 0$ & $nx \rightarrow 1$ & $i \rightarrow j$ & \\ & $(nx - 1) \rightarrow 1$ & $(nx - 1) \rightarrow 2$ & & $nx \rightarrow ny$ \\ \cline{1-3} & $(nx + 1) \rightarrow -1$ & $(nx + 1) \rightarrow -1$ & & \\ $\psi = w$ & $nx \rightarrow 0$ & $nx \rightarrow 0$ & & \\ & $(nx - 1) \rightarrow 1$ & $(nx - 1) \rightarrow 1$ & & \\ \hline \end{tabular}$

Constant Phase velocity

Setting c_ψ = c_max in (5) leads to a more simple radiation boundary condition (here e.g. for a left-right flow along positive x-direction):

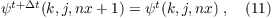
$\psi^{t + \Delta t}(k,j,nx+1) = \psi^{t}(k,j,nx) \; , \quad (11)$

with ψ = {u,v,w}. This formulation of the radiation boundary condtions saves computational time compared to the formulation of equations (7) to (10). Although, Orlanski (1976) suggested that this approach of radiation boundary condition leads to reflection for waves smaller than c_max which may occur in complex geophysical flows, our simulations of a convective boundary layer with background wind have been stable so far.

Mass flux correction

PALM offers the possibility of a mass flux correction at the outflow (e.g. Tian, 2004). If parameter conserve_volume_flow is set true, the mass flux at the inflow and outflow is calculated by:

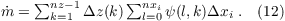
$\dot{m} = \sum_{k=1}^{nz-1} \Delta z(k) \sum_{l=0}^{nx_i} \psi(l,k) \Delta x_i \; . \quad (12)$

where Δx_i and ψ is equal to Δy (Δx) and u (v) in case of bc_lr (bc_ns). The correction factor for the outflow velocity, which is necessary due to different mass fluxes at inflow and outflow, can be calculated by

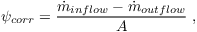
$\psi_{corr} = \dfrac{\dot{m}_{inflow} - \dot{m}_{outflow}}{A} \; ,$

where A is the area of the boundary

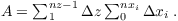
$A = \sum_1^{nz-1} \Delta z \sum_0^{nx_i} \Delta x_i \; .$

The streamwise velocity at the outflow is corrected by adding ψ_corr at each grid point of the outflow between bottom and top (k=1:nz), in order to guarantee that the mass leaving the domain exactly balances the one entering it.

References

Davies, H. C., 1976: A lateral boundary formulation for multi-level prediction models. Quart. J. R. Met. Soc., 102, 405-418.

Fröhlich, F., 2006: Large eddy simulation turbulenter Strömungen. B.G. Teubner Verlag, 414 pp.

Orlanski, I., 1976: A simple boundary condition for unbounded hyperbolic flows. J. Comput. Phys., 21, 251-269.

Raymond, W. H. and H. L. Kuo, 1984: A radiation boundary condition for multi-dimensional flows. Quart. J. R. Met. Soc., 110, 535-551.

Tian, W., Z. Guo and R. Yu, 2004: Treatment of LBCs in 2D simulation of convection over hills. Adv. Atmos. Sci., 21, No. 4, 573-586.

Yoshida, T. and T. Watanabe, 2010: Sommerfeld radiation condition for incompressible viscous flows. 5th European Conference on Computational Fluid Dynamics, 14-17 June, Lisbon, Portugal, ECCOMAS, 1-11.