| Version 8 (modified by maronga, 9 years ago) (diff) |
|---|
Land surface model
Overview
Since r1551 a full land surface model (LSM) is available in PALM. It consists of a four layer soil model, predicting soil temperature and moisture content, and a solver for the energy balance of the skin surface layer. Moreover, a liquid water reservoir accounts for the presence of liquid water on plants and soil due to precipitation. The implementation is based on the ECMWF-IFS land surface parametrization (H-TESSEL) and its adaptation in the DALES model (Heus et al. 2010).
Note that the use of the LSM requires using a radiation model to provide radiative fluxes at the surface.
Energy balance solver
The energy balance of the Earth's surface reads
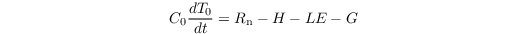
where C0 and T0 are the heat capacity and radiative temperature of the surface skin layer, respectively. Rn, H, LE, and G are the net radiation, sensible heat flux, latent heat flux, and ground (soil) heat flux at the surface, respectively. H is calculated as
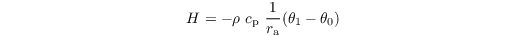
where ρ is the density of the air, cp = 1005 J kg-1 K-1$ is the specific heat at constant pressure, ra is the aerodynamic resistance, and θ0 and θ1 are the potential temperature at the surface and at the first grid level above the surface, respectively. ra is calculated via Monin-Obukhov similarity theory, based on roughness lengths for heat and momentum and the assumption of a constant flux layer between the surface and the first grid level.
G is parametrized as (Duynkerke 1999)
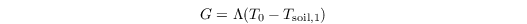
with Λ being the heat conductivity between skin layer and the soil, and Tsoil,1 being the temperature of the uppermost soil layer. The latent heat flux is calculated as
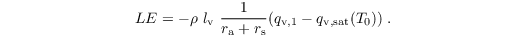
Here, lv = 2.5 * 106 J kg-1 is the latent heat of vaporisation, rs is the surface resistance, qv,1 is the specific humidity at first grid level, and qv,sat is the saturation specific humidity at temperature T0.
All equations above are solved locally for each surface element of the LES grid. Each element can consist of both patches of bare soil, vegetation, and a liquid water reservoir, which is the interception water stored on plants and soil from precipitation. Therefore, an additional equation is solved for the liquid water reservoir. LE is then calculated for each of the three components (bare soil, vegetation, liquid water). The resistances are calculated following Jarvis (1976).
C0 is set to zero, the energy balance is solved implicitly by linearising qv,sat.
Soil model
Technical details
The discretized and linearized energy budget equation in PALM reads
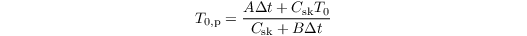
with
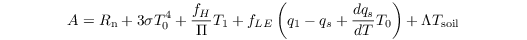
and
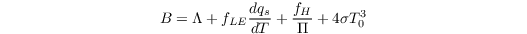
with (in order of occurence):

Usage
References
Attachments (2)
-
2015_LSM.pdf
(2.8 MB) -
added by maronga 10 years ago.
LSM introduction
-
wall_concept_type1.png
(34.1 KB) -
added by maronga 8 years ago.
soil model (vegetation)
