| Version 26 (modified by maronga, 9 years ago) (diff) |
|---|
Land surface model
Overview
Since r1551 a full land surface model (LSM) is available in PALM (see land_surface_model_mod.f90). It consists of a four layer soil model, predicting soil temperature and moisture content, and a solver for the energy balance, predicting the temperature of the skin layer. Moreover, a liquid water reservoir accounts for the presence of liquid water on plants and soil due to precipitation. The implementation is based on the ECMWF-IFS land surface parametrization (H-TESSEL) and its adaptation in the DALES model (Heus et al. 2010).
Note that the use of the LSM requires using some kind of radiation model to provide radiative fluxes at the surface.
Energy balance solver
The energy balance of the Earth's surface reads
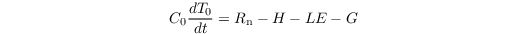
where C0 and T0 are the heat capacity and radiative temperature of the surface skin layer, respectively. Rn, H, LE, and G are the net radiation, sensible heat flux, latent heat flux, and ground (soil) heat flux at the surface, respectively.
Parameterization of H
H is calculated as
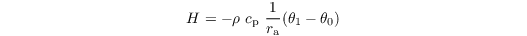
where ρ is the density of the air, cp = 1005 J kg-1 K-1 is the specific heat at constant pressure, ra is the aerodynamic resistance, and θ0 and θ1 are the potential temperature at the surface and at the first grid level above the surface, respectively. ra is calculated via Monin-Obukhov similarity theory, based on roughness lengths for heat and momentum and the assumption of a constant flux layer between the surface and the first grid level:
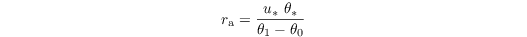
where u* and θ* are the friction velocity and the characteristic temperature scale according to Monin-Obukhov similarity scaling (these are calculated in surface_layer_fluxes.f90).
Parameterization of G
G is parametrized as (see Duynkerke 1999)
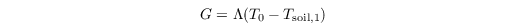
with Λ being the heat conductivity between skin layer and the soil, and Tsoil,1 being the temperature of the uppermost soil layer.
Parameterization of LE
The latent heat flux is calculated as
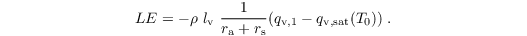
Here, lv = 2.5 * 106 J kg-1 is the latent heat of vaporisation, rs is the surface resistance, qv,1 is the specific humidity at first grid level, and qv,sat is the saturation specific humidity at temperature T0.
All equations above are solved locally for each surface element of the LES grid. Each element can consist of both patches of bare soil, vegetation, and a liquid water reservoir, which is the interception water stored on plants and soil from precipitation. Therefore, an additional equation is solved for the liquid water reservoir. LE is then calculated for each of the three components (bare soil, vegetation, liquid water). The resistances are calculated separately for bare soil and vegetation following Jarvis (1976). The canopy resistance is calculated as
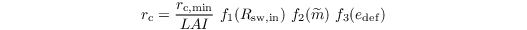
with

The correction functions read
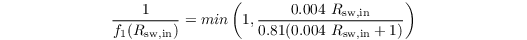
which accounts for the reaction of plants to shortwave radiation (opening/closing stomata),
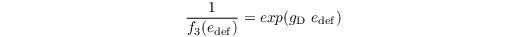
where gD is a correction factor (for high vegetation only, otherwise zero). Moreover, the reaction of plants to water availability in the soil is considered:
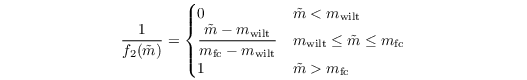
where

and
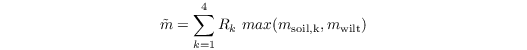
where
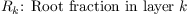
The bare soil resistance is given by
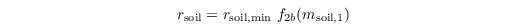
with
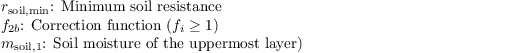
The total evapotranspiration is then calculated as
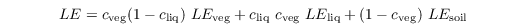
where cveg, and cliq is the surface fraction covered with vegetation and liquid water, respectively.
Prognostic equation for the liquid water reservoir
The prognostic equation for the liquid water stored on plants and bare soil mliq reads
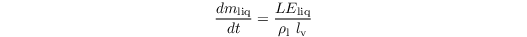
For positive values of LEliq, liquid water is evaporating from the surface, while negative values indicate precipitation (rain, dew).
Soil model
The soil model consists of prognostic equations for the soil temperature and the volumetric soil moisture which are solved for multiple layers. The soil model only takes into account vertical transport within the soil and no ice phase is considered. By default, the soil model consists of four layers (see figure below), in which the vertical heat and water transport is modelled using the Fourier law of diffusion and Richards' equation, respectively. Also, root fractions can be assigned to each soil layer to account for the explicit water withdrawal of plants used for transpiration from the respective soil layer.
Soil heat transport
The prognostic equation for soil temperature reads
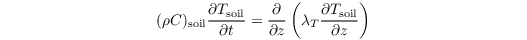
with

The volumetric heat capacity is calculated as
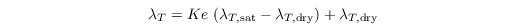
with
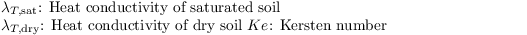
The heat conductivity of saturated soil is given by
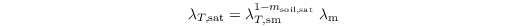
with
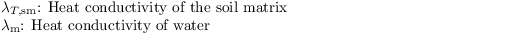
The Kersten number is calculated as
![\begin{equation*}
Ke = \log_{10} \left[max\left(0.1, \dfrac{m_\mathrm{soil}}{m_\mathrm{sat}}\right) \right] + 1
\end{equation*}](/trac/tracmath/e77050c1b4636f38bc44df22df92578fe40c737a.png)
Soil moisture transport
The prognostic equation for volumetric soil moisture reads
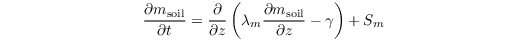
with
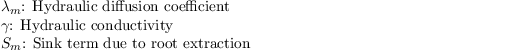
The hydraulic diffusion coefficient is calculated after Clapp and Hornberger (1978) as
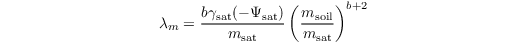
with
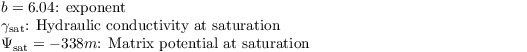
The hydraulic conductivity is calculated either after Van Genuchten (1980) (as in H-TESSEL):
![\begin{equation*}
\gamma = \gamma_\mathrm{sat} \dfrac{\left[(1 + (\alpha h)^n)^{1 - 1/n} - (\alpha h)^{n-1}\right]^2}{(1+ (\alpha h)^n)^{(1 - 1/n)(l + 2)}}
\end{equation*}](/trac/tracmath/5b600b1408ec0ddcff47d3193cf9bc73e809981f.png)
where

and
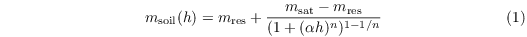
or after Clapp and Hornberger (1978):
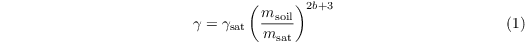
Root extraction
The root extraction of water from the respective soil layer Sm is calculated as follows:
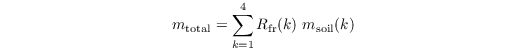
where mtotal is the total water content of the soil and Rfr is the root fraction in soil layer k'. Only those layer are summed up which have a soil moisture above wilting point (plants do not extract water from such layers). The root profiles must prescribed in such a way that #!Latex \begin{equation*} \sum \limits_{k = 1}4 R_\mathrm{fr}(k) = 1 \end{equation*} }}} The root extraction is then given by
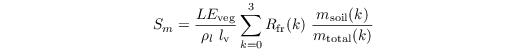
Again, only layers where the soil moisture is above its value at wilting point are used for root extraction (which is zero otherwise).
Boundary conditions
Neumann boundary conditions are used for the transport of heat and moisture at the upper boundary (surface). The values are given by the energy balance in terms of G for heat and LEsoil, for moisture. At the bottom boundary a deep soil temperature is prescribed (Dirichlet conditions), whereas two options are available for soil moisture. The underlying surface can be set to either bedrock (no moisture flux at the bottom, water conserving) or to open bottom (implies non-conservation of water).
For more details, see also Viterbo et al. (1995) and Balsamo et al. (2009).
Technical details
The discretized and linearized energy budget equation in PALM reads
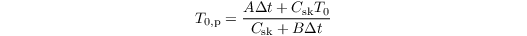
with
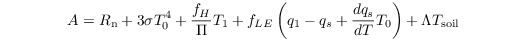
and
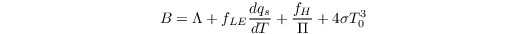
with (in order of occurence):

Time stepping is the same as in the atmospheric part of the model (default: 3rd-order Runge-Kutta).
Note that for Csk = 0, the prognostic equation for T0,p reduces to a diagnostic equation:
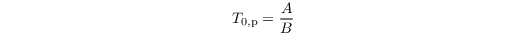
Usage
References
- Balsamo G, Vitebo P, Beljaars A, van den Hurk B, Hirschi M, Betts AK, Scipal K. 2009. A revised hydrology for the ECMWF model: Verification from field site to terrestrial water storage and impact in the integrated forecast system. J. Hydrometeorol. 10: 623–643.
- Clapp, RB and Hornberger GM. 1978. Empirical Equations for Some Soil Hydraulic Properties. Water Res. Res., 14: 601-604.
- Duynkerke PG. 1999. Turbulence, radiation and fog in Dutch stable boundary layers. Boundary-Layer Meteorol. 90: 447–477, doi:10.1023/A:1026441904734.
- Heus T, Van Heerwaarden CC, Jonker HJJ, Siebesma AP, Axelsen S, Dries K, Geoffroy O, Moene AF, Pino D, De Roode SR, Vil`a-Guerau de Arellano J. 2010. Formulation of the dutch atmospheric large-eddy simulation (dales) and overview of its applications. Geosci. Model Dev. 3: 415–444.
- Jarvis PG. 1976. The interpretation of the variations in leaf water potential and stomatal conductance found in canopies in the field. Philos. Trans. Roy. Soc. London 273B: 593–610.
- van Genuchten M. 1980. A closed form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Amer. J. 44: 892–898.
- Viterbo P, Beljaars ACM. 1995. An Improved Land Surface Parameterization Scheme in the ECMWF Model and Its Validation. J. Climate 8: 2716–2748.
Attachments (2)
-
2015_LSM.pdf
(2.8 MB) -
added by maronga 10 years ago.
LSM introduction
-
wall_concept_type1.png
(34.1 KB) -
added by maronga 8 years ago.
soil model (vegetation)
