Boundary conditions

Constant flux layer

Basics

Following Monin-Obukhov similarity theory (MOST) a constant flux layer can be assumed as boundary condition between the surface and the first grid level where scalars and horizontal velocities are defined (k = 1, z_MO = 0.5 Δz). It is then required to provide the roughness lengths for momentum z₀ and heat z_0,h. Momentum and heat fluxes as well as the horizontal velocity components are calculated using the following framework. The formulation is theoretically only valid for horizontally-averaged quantities. In PALM we assume that MOST can be also applied locally and we therefore calculate local fluxes, velocities, and scaling parameters.

Following MOST, the vertical profile of the horizontal wind velocity

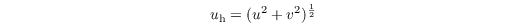
is given in the surface layer by

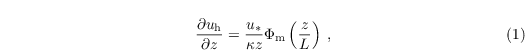
where κ = 0.4 is the Von Kármán constant and Φ_m is the similarity function for momentum in the formulation of Businger-Dyer (see e.g. Panofsky and Dutton 1984)

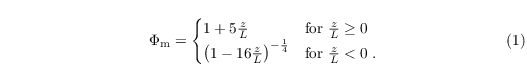
Here, L is the Obukhov length, calculated as

(eq:L) 

The scaling parameters θ_* and q_* are defined by MOST as:

(eq:scales)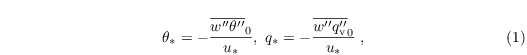 

with the friction velocity u_* defined as

In PALM, u_* is calculated from u_h at z_MO by vertical integration over z from z₀ to z_MO.

From the equations above it is possible to derive a formulation for the horizontal wind components, viz.

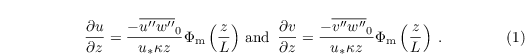
Vertical integration of the above equation over z from z₀ to z_MO then yields the surface momentum fluxes

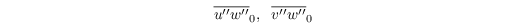
The formulations above all require knowledge of the scaling parameters θ_* and q_*. These are deduced from vertical integration of

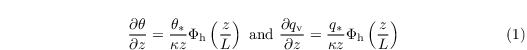
over z from z_0,h to z_MO. The similarity function Φ_h is given by

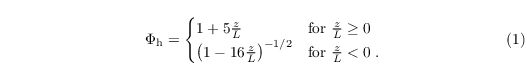
Implementation

Currently, there are three different options to calculate the Obukhov length and the surface fluxes which are steered via the NAMELIST parameter most_method.

Method 1: circular

The traditional implementation in PALM (most_method = 'circular') requires the use of data from the previous time step. The following steps are thus carried out in sequential order. First of all, θ_* and q_* are calculated by integration using the value of z_MO/L from the previous time step. Second, the new value of z_MO/L is derived using the new values of θ_* and q_* but using u_* from the previous time step. Then, the new values of u_*, and subsequently the momentum fluxes are calculated by integration, respectively. At last, the new surface fluxes are derived from θ_* and q_*, and u_*. In the special case, when surface fluxes are prescribed instead of surface temperature and humidity, the first and last steps are omitted and θ_* and q_* are directly calculated from u_* and the surface fluxes.

In summary, the following actions are performed in sequential order:

1. calculate θ_* and q_*
2. calculate u_h
3. determine Obukhov length
4. calculate u_*
5. derive surface fluxes

Method 2: Newton iteration / lookup table

Alternatively, the Obukhov length can be calculated by solving an implicit equation relating the L to the bulk Richardson number. This can be achieved either by a Newton iteration algorithm (most_method = 'newton') or by using a lookup table (most_method = 'lookup'). Note that the latter is the new default in PALM as it is much faster than the Newton iteration method and the results are more precise compared to the circular method. However, it can only be used when the roughness lengths are homogeneously set on each processor.

Both methods require a different sequential order to derive the surface fluxes:

1. calculate u_h
2. determine Obukhov length (Newton iteration or lookup table)
3. calculate u_*
4. calculate θ_* and q_*
5. derive surface fluxes

Depending on whether Neumann (prescribed fluxes) or Dirichlet boundary conditions are used for temperature and humidity, the bulk Richardson number is related to the Obukhov length via

where

In case of most_method = 'newton', the above equations are solved for L by Newton iteration, i.e. finding the root of the equation

where x and y depend on the chosen boundary conditions (see above). The solution is given by iteration of

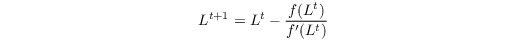
with #!Latex \begin{equation*} f'(L) = \dfrac{df}{dL} \end{equation*} }}} until L meets a convergence criterion.

If most_method = 'lookup' is used, a table of Ri_\mathrm{b} against z_MO/L is created at model start, based on the prescribed values of the roughness lengths. During the model run, Ri_\mathrm{b} is calculated and the respectively value of z_MO/L is retrieved from the lookup table and using linear interpolation between the discrete values in the table. In order to speed up this method, the value of Ri_\mathrm{b} from the previous time step is used as initial value. Due to the fact that the lookup table is created at model start, it is essential that the roughness lengths are 1) homogeneous on each processor (limiting this method to homogeneous surface configurations) and should not vary during the simulation (should thus not be used when using dynamic roughness length over water surfaces).

For more details, see surface_layer_fluxes.f90.