doc/tec/lsf – PALM

Home

Context Navigation

Large scale forcing

Usually, the LES model PALM is used to simulate the flow in the boundary layer which is a certain part of the atmosphere. Processes occurring on larger scales than those in the boundary layer including large scale advection of scalars, large scale pressure gradients or large scale subsidence have also to be considered in the model, especially when focusing on realistic situations observed during measurement campaigns. In limited domain models with non-cyclic boundary conditions the large scale state enters through the boundary conditions at the lateral walls, and is usually taken from larger-scale models. This method isn't possible with cyclic horizontal boundary conditions (because there are no real lateral boundaries). In case of cyclic boundary conditions PALM uses a method developed by Neggers et al. (2012), which is switched on by parameter large_scale_forcing. This method does not work with non-cyclic horizontal boundary conditions! Furthermore, it requires to use a flat topography. In case of cyclic boundary conditions, this forcing is prescribed homogeneously in the horizontal directions and thus depends on height and time only. The relation between larger scales (LS) pressure (p_LS) gradient and geostrophic wind is given by

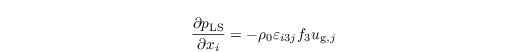
$\begin{align*} \frac{\partial p_{\text{LS}}}{\partial x_{i}}=-\rho_{0}\varepsilon_{i3j}f_{3}u_{\mathrm{g},j} \end{align*}$

and enters the first equation in Sect. governing equations.
LS vertical advection (subsidence or ascent) tendencies can be prescribed for the scalar prognostic variables φ ∈ {θ, q, s} by means of

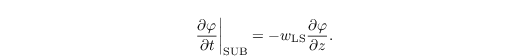
$\begin{align*} \left.\frac{\partial \varphi}{\partial t}\right\vert_{\text{SUB}} = -w_{\text{LS}}\frac{\partial \varphi}{\partial z}. \end{align*}$

The so-called subsidence velocity w_LS and the geostrophic wind components u_g and v_g can either be prescribed gradient-wise or they can be provided in an external file. Moreover, an external pressure gradient can be applied for simulations with Coriolis force switched off, which is usually required for simulations to be compared with wind tunnel experiments.
To account for less-idealized flow situations, time-dependent surface fluxes (or surface temperature and humidity) can be prescribed. Moreover, LS horizontal advective (LSA) tendencies can be added to the scalar quantities by means of

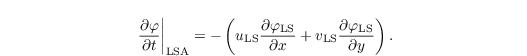
$\begin{align*} & \left.\frac{\partial \varphi}{\partial t}\right\vert_{\text{LSA}} = -\left(u_{\text{LS}}\frac{\partial \varphi_{\text{LS}}}{\partial x}+v_{\text{LS}}\frac{\partial \varphi_{\text{LS}}}{\partial y}\right). \end{align*}$

These tendencies are typically derived from larger scale models or observations and should be spatially averaged over a~large domain so that local-scale perturbations are avoided.
Newtonian relaxation (nudging) towards given large-scale profiles φ_LS can be used for φ ∈ {u, v, θ, q, s} via

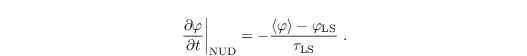
$\begin{align*} \left.\frac{\partial \varphi}{\partial t}\right\vert_{\text{NUD}} = -\frac{\left\langle\varphi\right\rangle-\varphi_{\text{LS}}}{\tau_{\text{LS}}}\;. \end{align*}$

τ_LS is a relaxation time-scale which, on the one hand, should be chosen large enough in the order of several hours to allow an undisturbed development of the small-scale turbulence in the LES model. On the other hand, it should be chosen small enough to account for synoptic disturbances (Neggers et al., 2012). In this way, the nudging can prevent considerable model drift in time. For additional information about nudging see Sect. nudging.

Examples

A complete example for a PALM run with large scale forcing (and nudging) is documented here.

References

* Neggers RAJ, Siebesma AP, Heus T. 2012. Continous single-column model evaluation at a permanent meteorological supersite. Bull. Amer. Meteor. Soc. 29: 91-115. doi

Last modified 3 years ago Last modified on Feb 23, 2021 3:33:09 PM

Download in other formats:

Plain Text