Home


About us
PALM
PALM-4U
Installation
Release notes
Documentation
Getting Help
Gallery
Developers area

Higher order advection scheme

Based on a flux formulation of the advection term

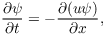
$\dfrac{\partial \psi}{\partial t} = -\dfrac{\partial ( u \psi )}{\partial x},$

the one dimensional advection equation can be written in the following semidiscrete form:

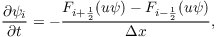
$\dfrac{\partial \psi_{i} }{\partial t} = - \dfrac{F_{i+\frac{1}{2}}(u\psi) - F_{i-\frac{1}{2}}(u\psi)}{\Delta x},$

where

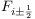
$F_{i\pm\frac{1}{2}}$

denotes the fluxes staggered half a grid length related to the advected quantity.
Wicker and Skamarock (2002) discretized the 6th and 5th order fluxes as follows:

$F_{i-\frac{1}{2}}^{6} = \frac{u_{i-\frac{1}{2}}}{60} \left[ 37(\psi_{i}+\psi_{i-1}) - 8(\psi_{i+1} + \psi_{i-2}) +(\psi_{i+2} + \psi_{i-3}) \right] ,$

$F_{i-\frac{1}{2}}^{5} = F_{i-\frac{1}{2}}^{6} - \dfrac{|u_{i-\frac{1}{2}}|}{60} \left[10(\psi_{i}-\psi_{i-1}) -5(\psi_{i+1} - \psi_{i-2})+(\psi_{i+2} - \psi_{i-3}) \right] . $

The 5th order upwind discretization (WS5) consists of a centered non dissipative 6th (WS6) order flux and an artificially added numerical dissipation term. This term is necessary to stabilize the numerical solution, because higher order centered fluxes exhibits worse stability properties. The absolute value of the advective velocity component in the dissipation term removes a sign-dependent effect of the velocity and assures a dissipative effect also for u < 0.

Numerical properties

A semidiscrete fourier transformation for the spatial derivatives maps the one dimensional advection equation in fourier space as follows (Baldauf, 2008):

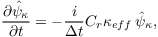
$\dfrac{\partial \hat{\psi}_{\kappa}}{\partial t} = - \dfrac{i}{\Delta t} C_{r} \kappa_{eff}\,\hat{\psi}_{\kappa},$

where

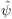
$\hat{\psi}$

denotes the fourier transformed of ψ. The Courant number

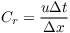
$C_{r} = \dfrac{u \Delta t}{\Delta x}$

characterizes stability properties and i is the imaginary unit. κeff is the effective wavenumber of a mode in fourier space and characterizes the modified wavenumber through the discretization. The real part of the effective wavenumber describes the dispersion error, the imaginary part the dissipation error.

num_prop
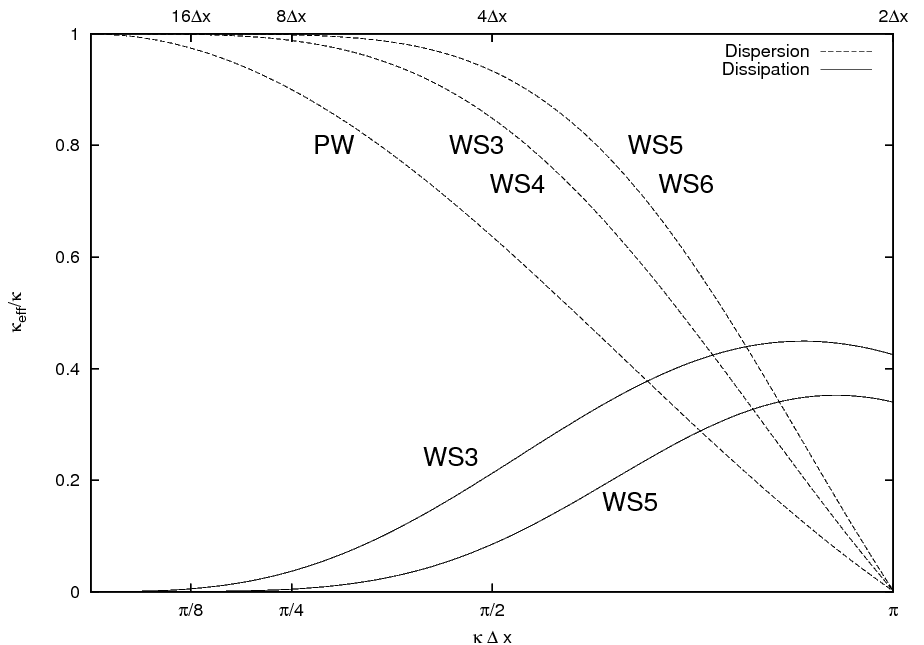
Fig. 1 shows the dispersion and dissipation error as a function of the dimensionless wavenumber κ Δx for WS3 (3rd order scheme), WS4 (4th order scheme), WS5, WS6 and the 2nd order scheme of Piacsek and Williams (1970) (PW). The dispersion error of the upwind schemes and the dispersion error of the next higher, even ordered scheme are identical. Generally the dispersion error decreases with increasing order of the discretization. However, no of the depicted schemes is able to adequately resolve structures with wavelengths near 2-Δx (generally no scheme based on finite differences is capable to do this). The centered, even ordered schemes hold no dissipation errors. With increasing order the numerical dissipation is more local. So the maximum wavelength affected by the dissipation term is round about 8-Δx with WS5, whereas wavelength of 16-Δx are still affected with WS3. Accordingly to the maximum of the amplification factor at κ Δx = 1.69 (these waves become unstable at first) in conjunction with the used Runge-Kutta method (Baldauf, 2008), the 5th order dissipation is sufficient to avoid instabilities. The maximum stable Courant-number is Cr = 1.4 (Baldauf, 2008).

Note: A stable numerical solution can only be guaranteed with the 3 rd order Runge-Kutta method.

Boundaries

Due to the large stencil of WS5, additional ghost layers are necessary on each lateral boundary of each processor subdomain to avoid local data dependencies. Therefore, the exchange of ghost layers is adapted to a dynamic number of ghost layers. For the bottom and top boundaries, lateral non-cyclic boundaries as well as near topography walls the order of the discrertization is successively degraded from WS5 to WS3 to a 1st order scheme. The degradation is controlled by three-dimensional bit flags, where several bits mark the order of the advection scheme in the x-, y-, and z-direction. Technically, in case of topography, advective fluxes are calculated for the first-, third-, and fifth-order discretization at each grid point, while the respective bit controls which discretization is finally used. In the following, the respective flags are listed:

Array Bit Meaning

wall_flags_0

0

scalar advection in the x-direction: first order

wall_flags_0

1

scalar advection in the x-direction: third order

wall_flags_0

2

scalar advection in the x-direction: fifth order

wall_flags_0

3

scalar advection in the y-direction: first order

wall_flags_0

4

scalar advection in the y-direction: third order

wall_flags_0

5

scalar advection in the y-direction: fifth order

wall_flags_0

6

scalar advection in the z-direction: first order

wall_flags_0

7

scalar advection in the z-direction: third order

wall_flags_0

8

scalar advection in the z-direction: fifth order

wall_flags_0

9

u advection in the x-direction: first order

wall_flags_0

10

u advection in the x-direction: third order

wall_flags_0

11

u advection in the x-direction: fifth order

wall_flags_0

12

u advection in the y-direction: first order

wall_flags_0

13

u advection in the y-direction: third order

wall_flags_0

14

u advection in the y-direction: fifth order

wall_flags_0

15

u advection in the z-direction: first order

wall_flags_0

16

u advection in the z-direction: third order

wall_flags_0

17

u advection in the z-direction: fifth order

wall_flags_0

18

v advection in the x-direction: first order

wall_flags_0

19

v advection in the x-direction: third order

wall_flags_0

20

v advection in the x-direction: fifth order

wall_flags_0

21

v advection in the y-direction: first order

wall_flags_0

22

v advection in the y-direction: third order

wall_flags_0

23

v advection in the y-direction: fifth order

wall_flags_0

24

v advection in the z-direction: first order

wall_flags_0

25

v advection in the z-direction: third order

wall_flags_0

26

v advection in the z-direction: fifth order

wall_flags_0

27

w advection in the x-direction: first order

wall_flags_0

28

w advection in the x-direction: third order

wall_flags_0

29

w advection in the x-direction: fifth order

wall_flags_0

20

w advection in the y-direction: first order

wall_flags_0

31

w advection in the y-direction: third order

wall_flags_00

0

w advection in the y-direction: fifth order

wall_flags_00

1

w advection in the z-direction: first order

wall_flags_00

2

w advection in the z-direction: third order

wall_flags_00

3

w advection in the z-direction: fifth order

Statistical evaluation of turbulent fluxes

The statistical evaluation of turbulent fluxes should be consistent with the discretization in the prognostic equations because otherwise some unphysical effects occur. For example the computation of the turbulent fluxes as variances and covariances induces some conspicuous kinks in the vertical heat and momentum fluxes near the surface, while the temperature and velocity profiles show no conspicuity. In order to compute the turbulent fluxes as they appear in the prognostic equations, the fluxes are computed in the advection routines, buffered and then reused for the statistics. To receive the turbulent and not the mean signal and to remove the influence of Galilei transformation, the centered fraction of the flux Fi+1/2 has to be multiplied with a factor

\[ \frac{u_{i+\frac{1}{2}} - \overline u}{u_{i+\frac{1}{2}} - u_{i, Galilei}} \]

and the dissipative fraction with a factor

\[ \frac{|u_{i+\frac{1}{2}} - \overline u|}{|u_{i+\frac{1}{2}} - u_{i, Galilei}|}, \]

where u denotes the corresponding velocity component. Furthermore, the turbulent fluxes are evaluated on each Runge-Kutta substep and weighted with the respective Runge-Kutta coefficients to remove dependencies of the Runge-Kutta substeps. The interpretation of the turbulent fluxes as variances and covariances is no longer valid when using WS5. For other advection schemes, like the PW-scheme, the interpretation of turbulent fluxes as co/variances is still valid, because the discretization is alike the computation of the co/variances.

References

  • Baldauf, M., 2008: Stability analysis for linear discretisations of the advection equation with Runge-Kutta time integration. J. Comput. Phys., 227, 6638-6659.
  • Piacsek, S. A. and G. P. Williams, 1970: Conservation properties of convection difference schemes. J. Comput. Phys., 198, 580-616.
  • Wicker, L. J. and W. C. Skamarock, 2002: Time-splitting methods for elastic models using forward time schemes. Mon. Wea. Rev., 130, 2088-2097.
Last modified 9 years ago Last modified on Nov 12, 2015 2:44:02 PM

Attachments (2)

Download all attachments as: .zip

                                                                                                                                                                                                                                                                                                                                                                               
  | Impressum | ©Leibniz Universität Hannover |