Urban surface model (USM)

Main page of the urban surface model under construction. Click here for first information about capabilities and model steering. Also available, the related article PALM-USM v1.0: A new urban surface model integrated into the PALM large-eddy simulation model (Resler et al., Geosci. Model Dev., 10, 3635–3659, ​10.5194/gmd-10-3635-2017 ​10.5194/gmd-10-3635-2017)

This page is part of the Urban Surface Mod (USM) documentation.
It describes the physical and numerical realization of the USM.
Please also see the namelist parameters.

Overview

Since r19xx an urban surface model (USM) is available in PALM (see urban_surface_mod.f90). It consists of a multi layer wall and soil model, predicting wall and soil temperature and moisture content, and a solver for the energy balance, predicting the temperature of the surface or the skin layer. Urban surfaces (building surfaces) are simulated using a tile approach. Each surface element consists of a fraction of bare wall/ roof, window and green elements (green roofs/ facades) with underlying soil layers (green roofs only) and a bare wall/ roof structure.

Energy balance solver

The energy balance of the urban surfaces reads

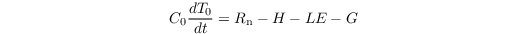
where C₀ and T₀ are the heat capacity and radiative temperature of the surface skin layer, respectively. Note that C₀ is usually zero as it is assumed that the skin layer does not have a heat capacity (see also below). R_n, H, LE, and G are the net radiation, sensible heat flux, latent heat flux, and ground (soil) heat flux at the surface, respectively.

The energy balance is calculated for each urban surface tile individually and the three radiation surface temperatures are combined together.

The parametrisation of the sensible heat flux, latent heat flux and ground heat flux of the wall/ window/ soil is equivalent to the Land Surface Model (LSM).

The wall heat and green heat model consist of prognostic equations for the bare, window and soil temperature and the volumetric soil moisture which are solved for multiple layers. The models only take transport into account that is orthogonal to the urban surface layer orientation and no ice phase is considered. By default, the wall heat model and the green heat soil model consists of four layers each (see Fig. 1 below), in which the orthogonal heat and water transport inside the soil is modelled.

Figure 1: urban surfaces (bare, window, green - horizontal and vertical) in PALM-4U

The physical properties of the urban surfaces and wall, window and green soil elements can be set using values from a building database where different types of buildings are defined. The insulation value of windows are there only characterized by the U-value and and the heat capacity and heat conductivity is evenly distributed (no real glas or gas layers are taken into account.

The green heat model calculates the transport of soil moisture but neglects the extraction of water from the respective soil layers.

Window transmissivity: representation

The radiant flux received by the window (incident radiant flux, Φ_I) is partially reflected back (Φ_R), partially absorbed by the mass of the glass (Φ_A which is simulated by four discretized layers of window depth) and partially transmitted through the window, where the transmitted flux Φ_T may be processed by the indoor model (if enabled), therefore

Most of the reflection happens as specular reflection on the frontal and rear boundary between the glass and air. The radiant flux reflected at the rear boundary is partially reflected again at the frontal boundary, then partially at the rear boundary again and so on, however, these fluxes are typically negligible, as are the non-specular reflections, the absorption of the reflected fluxes and the scattering inside the glass; a bias can be avoided by adjusting the parameters of the non-neglected processes. The reflected radiant flux can thus be simplified as Φ_R=Φ_RF+Φ_RR, where Φ_RF is the radiant flux reflected at the frontal boundary and Φ_RR is the radiant flux reflected at the rear boundary.

The total transmissivity T=Φ_T/Φ_I is the fraction of transmitted and received radiant flux, i.e. it includes loss by reflection and absorption together. The internal transmissivity T_I=Φ_TT/Φ_TI describes the loss by absorption by a single pass of the light through the glass, where Φ_TI=Φ_I-Φ_RF is the radiant flux entering the glass after frontal boundary reflection and Φ_TT=Φ_TI-Φ_A is the radiant flux leaving the glass before rear boundary reflection. The frontal reflectivity R_F=Φ_RF/Φ_I and rear reflectivity R_R=Φ_RR/Φ_TT express the fraction of radiant flux reflected at each boundary. Together, the radiant flux passing through the glass can be described sequentially as it is diminished by frontal reflection, absorption and rear reflection. (2) describes this process additively while (1) describes the fractions multiplicatively:

The internal transmissivity is described by the Beer–Lambert law. For a homogeneous material with width z, it is equal to

where a is the absorption (attenuation) coefficient.

Window transmissivity: modelling

The window fraction of surfaces in PALM is described by two parameters: albedo (total reflectivity in the respective band, R=Φ_R/Φ_I) and transmissivity (total, T).

The frontal and rear reflectivities of glass are similar. From simple Fresnel equations they are equal, in reality the frontal reflectivity is slightly stronger. In PALM they are modelled as equal and they are calculated from the total reflectivity.

Using R_F=R_R we get:

In order to simulate the absorption by the discretized window layers, the absorption coefficient has to be calculated from the parameters:

In the prognostic equations, the absorbed flux is added to the temperature tendency in the Runge–Kutta method for each layer l, depending on layer width and. The absorbed flux is equal to

where z_l-1 is the depth of the previous layer (cumulative width of all previous layers) and z_l is the depth of layer l.

Boundary conditions

Neumann boundary conditions are used for the transport of heat at the upper boundary (surface). The values are given by the energy balance. At the bottom boundary either a fixed temperature of the inner wall and window layers is set or the ground heat flux from the inner wall and window surface is used that is calculated by the indoor model (Dirichlet conditions).